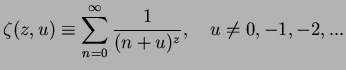Next: Validity of Markov Assumption
Up: Thermal Bath Correlation Function
Previous: Bosonic Spectral Density
Contents
Index
One can write
![$\displaystyle C(t) = \int_0^{\infty}
d\omega \rho(\omega) \left[\coth\left(\beta\omega/2\right) \cos(\omega t)
- i \sin(\omega t)\right],$](img238.png) |
|
|
(57) |
where we used the useful identity
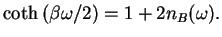 |
|
|
(58) |
Calculation of the integral with
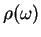 given by Eq.(7.54)
yields
given by Eq.(7.54)
yields
where 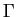 is the Gamma function
and
is the Gamma function
and
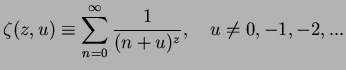 |
|
|
(60) |
is the generalised Zeta function (cf. W. Magnus, F. Oberhettinger, and
R. P. Soni, Formulas and Theorem for the
Special Functions of Mathematical Physics, Springer, Berlin 1966).
The zero temperature limit is obtained either from the
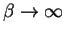 limit of Eq.(7.59) or directly by calculating the integral,
limit of Eq.(7.59) or directly by calculating the integral,
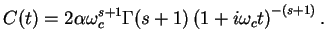 |
|
|
(61) |





Next: Validity of Markov Assumption
Up: Thermal Bath Correlation Function
Previous: Bosonic Spectral Density
Contents
Index
Tobias Brandes
2004-02-18
![$\displaystyle C(t) = \int_0^{\infty}
d\omega \rho(\omega) \left[\coth\left(\beta\omega/2\right) \cos(\omega t)
- i \sin(\omega t)\right],$](img238.png)