Revision: $P$-representation

We recall that the $P$-representation of an operator $\hat{\theta}$ was defined as (cf. 4.137)

$$\hat{\theta}= \int \frac{d^2 z}{\pi}P(\hat{\theta};z)\vert z\rangle \langle z\vert.$$ (69)

Remarks:

1. Other authors use a definition without the $1/\pi$.

2. Some books write $P(z)$ (instead of $P(\hat{\theta}=\rho;z)$) for the $P$-representation of the density operator, and use the form

$$P(z)\equiv P(z,z^*) = {\rm Tr} \left[\rho \delta(z^*-a^\dagger) \delta(z-a)\right].$$ (70)

(again multiply this by $\pi$ to get our $P$).

3. For coherent states $\rho=\vert z_0\rangle\langle z_0\vert$, one has $P(z)=\pi\delta(z-z_0)$.

4. We have the Metha-formula (4.149),

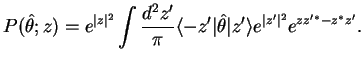$$P(\hat{\theta};z) = e^{\vert z\vert^2} \int \frac{d^2z'}{\pi} \langle -z'\vert \hat{\theta}\vert z'\rangle e^{\vert z'\vert^2} e^{zz'^*-z^*z'}.$$ (71)

5. The $P$-distribution can be highly singular. Example: number state.