Next: Solution of the PDE
Up: -representation
Previous: Revision: -representation
Contents
Index
In order to transform the master equation, we require the 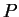 -representation of terms
like
-representation of terms
like
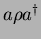 etc. Let us start with
etc. Let us start with
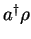 .
.
Method 1: We follow Walls/Milburn and introduce Bargmann states
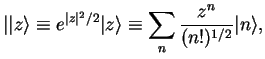 |
|
|
(72) |
(`coherent states without the normalisation factor in front').
Therefore,
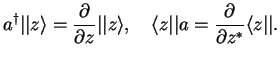 |
|
|
(73) |
We use this to write
using integration by parts,
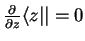 , and
assuming the vanishing of
, and
assuming the vanishing of 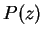 at infinity. Comparison yields
at infinity. Comparison yields
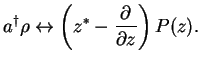 |
|
|
(75) |
Method 2: Use the Metha formula for
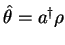 ,
,
Here, we generate 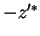 in the integral by differentiation with respect to the parameter
in the integral by differentiation with respect to the parameter 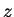 and subsequent compensation of the term aring from
and subsequent compensation of the term aring from 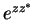 , thus arriving even faster
at Eq.(7.76). Similarly,
, thus arriving even faster
at Eq.(7.76). Similarly,
For the terms
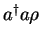 , the first method is easier:
, the first method is easier:
In particular, for the master equation we need
The whole master equation is therefore transformed into
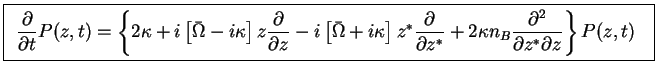 |
|
|
(78) |
Here, we have explicitely indicated that the 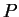 -function depends both on
-function depends both on 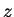 and on the time
and on the time 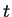 .
.
Remarks:
- The first order derivate terms are called drift terms, the second order
derivate terms diffusion term.
- This is not directly solvable by Fourier transformation:
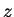 ,
,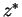 -dependence of coefficients.
-dependence of coefficients.
- Written in real coordinates, this has the form of a Fokker-Planck equation
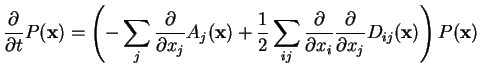 |
|
|
(79) |





Next: Solution of the PDE
Up: -representation
Previous: Revision: -representation
Contents
Index
Tobias Brandes
2004-02-18
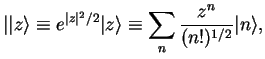
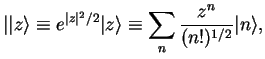
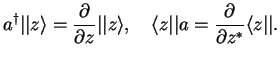
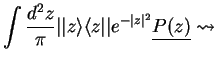
![$\displaystyle \int \frac{d^2 z}{\pi}a^{\dagger} \vert\vert z\rangle \langle z\v...
...tial z}
\vert\vert z\rangle \right] \langle z\vert\vert e^{-\vert z\vert^2}P(z)$](img304.png)
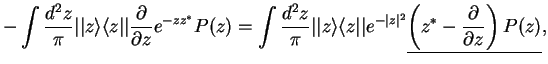
![]() ,
,
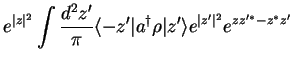
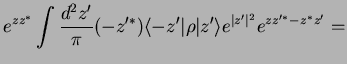
![$\displaystyle \left[ -\frac{\partial}{\partial z} + z^*\right]
(e^{zz^*}) \int ...
...\pi}
\langle -z'\vert \rho \vert z'\rangle e^{\vert z'\vert^2} e^{zz'^*-z^*z'}.$](img312.png)
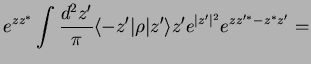
![$\displaystyle \left[ -\frac{\partial}{\partial z^*} + z\right]
(e^{zz^*}) \int ...
...\pi}
\langle -z'\vert \rho \vert z'\rangle e^{\vert z'\vert^2} e^{zz'^*-z^*z'}.$](img318.png)
![$\displaystyle \int \frac{d^2 z}{\pi}a^{\dagger} a \vert\vert z\rangle \langle z...
...l z}
\vert\vert z\rangle \right] \langle z\vert\vert e^{-\vert z\vert^2} z P(z)$](img321.png)
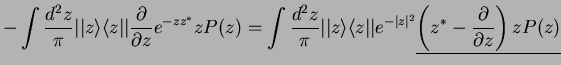
![$\displaystyle \int \frac{d^2 z}{\pi}\vert\vert z\rangle \langle z\vert\vert a^{...
...c{\partial}{\partial z^*}\langle z\vert\vert\right] e^{-\vert z\vert^2} z^*P(z)$](img324.png)
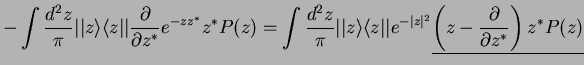
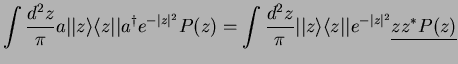
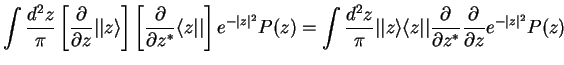
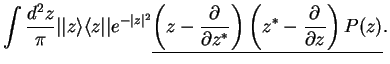
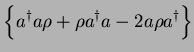
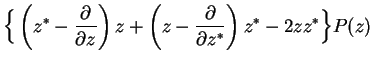
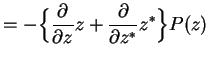
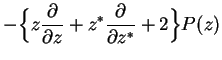
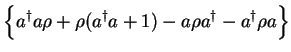
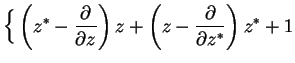
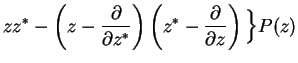
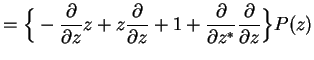
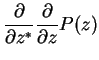
![$\displaystyle \left[-\frac{\partial}{\partial z}z + \frac{\partial}{\partial z^...
...ft[-z\frac{\partial}{\partial z} + z^*\frac{\partial}{\partial z^*}\right]P(z).$](img342.png)