Next: Remarks
Up: Master Equation IV: Phase
Previous: Solution of the PDE
Contents
Index
An alternative phase-space method is to convert the operator master equation into a PDE for the
Wigner function 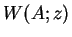 of an operator
of an operator 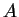 .
We recall Formula (4.177b) for the Wigner function of an operator product
.
We recall Formula (4.177b) for the Wigner function of an operator product 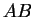 ,
,
![$\displaystyle W(AB;z)= W(A;z) \exp \left[
\frac{1}{2}\left(\overleftarrow{\part...
...erleftarrow{\partial}_{z^*} \overrightarrow{\partial}_{z} \right)\right] W(B;z)$](img418.png) |
|
|
(95) |
We obtain
Similarly,
Thus,
Therefore, the master equation Eq.(7.69) is converted into
We compare this with the PDE for the 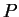 -function, Eq.(7.79):
-function, Eq.(7.79):
The difference is just in the diffusion term, i.e., 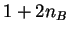 in the Wigner representation
instead of
in the Wigner representation
instead of 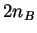 in the P representation. In the Wigner representation, even at zero temperature
in the P representation. In the Wigner representation, even at zero temperature
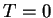 (
(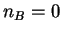 ) one has a diffusion term in the PDE. Technically, the solution proceeds as before:
one first solves the first order part via characteristics and then the diffusive part via
Fourier transformation.
) one has a diffusion term in the PDE. Technically, the solution proceeds as before:
one first solves the first order part via characteristics and then the diffusive part via
Fourier transformation.
- A similar derivation can be done for the
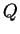 -representation, cf. Walls/Milburn.
The
-representation, cf. Walls/Milburn.
The 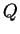 -representation is more convenient for systems where the
initial oscillator state is squeezed, or the decay is into a bath not in thermal equilibrium but
in a squeezed state.
-representation is more convenient for systems where the
initial oscillator state is squeezed, or the decay is into a bath not in thermal equilibrium but
in a squeezed state.





Next: Remarks
Up: Master Equation IV: Phase
Previous: Solution of the PDE
Contents
Index
Tobias Brandes
2004-02-18
![$\displaystyle W(AB;z)= W(A;z) \exp \left[
\frac{1}{2}\left(\overleftarrow{\part...
...erleftarrow{\partial}_{z^*} \overrightarrow{\partial}_{z} \right)\right] W(B;z)$](img418.png)
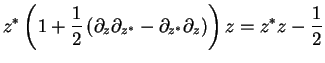
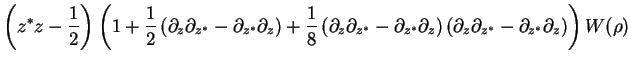
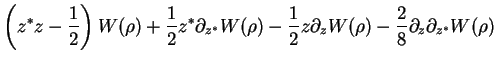
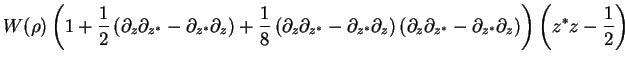
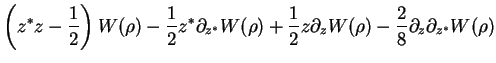
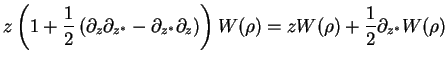
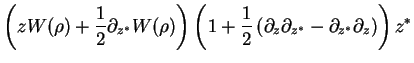
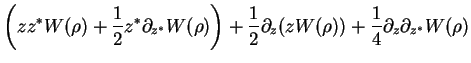
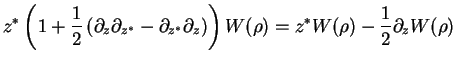
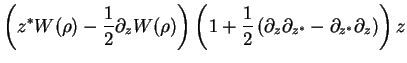
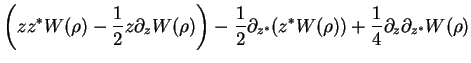
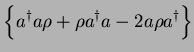
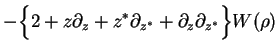
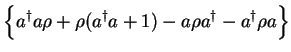
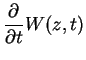
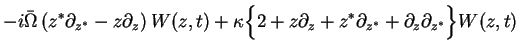
![$\displaystyle \left. i\left[ \bar{\Omega} - i\kappa\right]z\frac{\partial}{\par...
...z^*}
+\kappa[1+2 n_B] \frac{\partial^2}{\partial z^*\partial z}\right\} W(z,t).$](img446.png)