




Next: Expectation Values, Einstein Equations,
Up: Spontaneous Emission (Atom without
Previous: Model for : Two-Level
Contents
Index
We now use the fact that 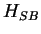 has the same form as for the the damped single bosonic mode if we identify
has the same form as for the the damped single bosonic mode if we identify
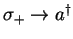 ,
,
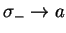 . We can therefore `copy' the derivation of the
master equation of the damped harmonic oscillator, as long as no commutation relations are used!
This is the case up to Eq.(7.46),
. We can therefore `copy' the derivation of the
master equation of the damped harmonic oscillator, as long as no commutation relations are used!
This is the case up to Eq.(7.46),
The interaction picture for the two-level atom is with respect to the Hamiltonian
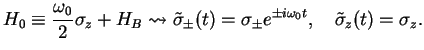 |
|
|
(125) |
In the interaction picture, the Master equation for the two-level atom therefore reads
We now use
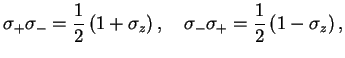 |
|
|
(127) |
re-arrange and transform back into the Schrödinger picture,
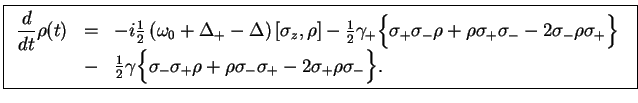 |
|
|
(128) |
We recall (note that the harmonic oscillator frequency 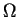 has to be replaced
by
has to be replaced
by 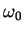 )
)
Remarks:
- In contrast to the harmonic oscillator, the energy shift
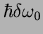 is now
temperature dependent.
is now
temperature dependent.
- The
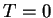 contribution is the Lamb-shift within RWA.
contribution is the Lamb-shift within RWA.





Next: Expectation Values, Einstein Equations,
Up: Spontaneous Emission (Atom without
Previous: Model for : Two-Level
Contents
Index
Tobias Brandes
2004-02-18
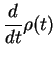
![$\displaystyle \frac{1}{2}\Big\{ \left[(\gamma_+ + 2 i \Delta_+)a^{\dagger} a
+ (\gamma + 2i \Delta) a a^{\dagger}\right]{\rho}(t)$](img562.png)
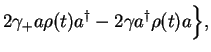 harmonic oscillator
harmonic oscillator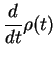
![$\displaystyle \frac{1}{2}\Big\{ \left[(\gamma_+ + 2 i \Delta_+)a^{\dagger} a
+ (\gamma + 2i \Delta) a a^{\dagger}\right]{\rho}(t)$](img562.png)
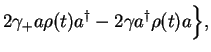 harmonic oscillator
harmonic oscillator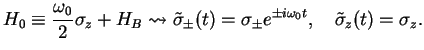
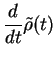
![$\displaystyle -\frac{1}{2}\Big\{ \left[(\gamma_+ + 2 i \Delta_+) \sigma_+ \sigma_-
+ (\gamma + 2i \Delta) \sigma_-\sigma_+ \right]\tilde{\rho}(t)$](img566.png)
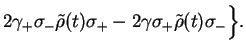
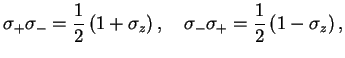
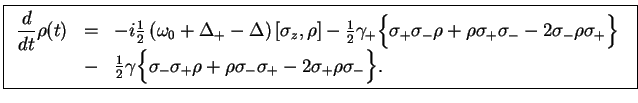
![$\displaystyle \delta \omega_0 \equiv
P\int_{0}^{\infty}d\omega\frac{\rho(\omega)[1+2n_B(\omega)] }{\omega_0-\omega}.$](img574.png)