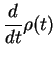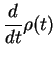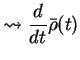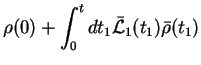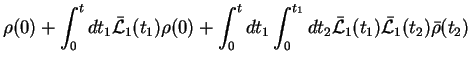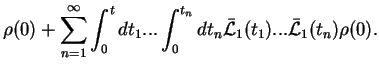Next: `Monte Carlo' Procedure
Up: Unravelling and Decomposition into
Previous: Super-Operators
Contents
Index
We may write the Master equation Eq.(7.143) as
This can be formally solved as follows: we define
Transforming back to 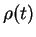 , we can explicitely write this as
, we can explicitely write this as
where we defined the un-normalised, conditioned `density matrix'
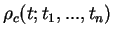 at time
at time 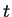 with
with 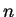 quantum jumps occuring at times
quantum jumps occuring at times
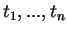 .
This object (the underlined term in Eq.(7.150))
indeed corresponds to the original density matrix
.
This object (the underlined term in Eq.(7.150))
indeed corresponds to the original density matrix 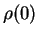 , `freely' time-evolved
with the effective Hamiltonian
, `freely' time-evolved
with the effective Hamiltonian
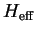 during the time intervals
during the time intervals
![$ (0,t_n]$](img648.png) ,
,
![$ (t_n,t_{n-1}]$](img649.png) ,... interrupted by
,... interrupted by 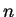 `jumps' at times
`jumps' at times 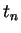 ,
, 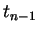 , ...,
, ..., 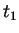 .
The total density matrix
.
The total density matrix 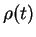 at time
at time 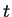 then is the sum over all
possible `trajectories' with
then is the sum over all
possible `trajectories' with
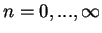 jumps occuring in between a `free',
effective time evolution.
jumps occuring in between a `free',
effective time evolution.





Next: `Monte Carlo' Procedure
Up: Unravelling and Decomposition into
Previous: Super-Operators
Contents
Index
Tobias Brandes
2004-02-18