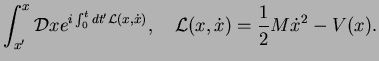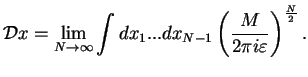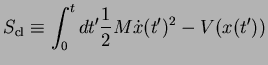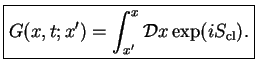Next: Double Path Integrals
Up: Feynman-Vernon Influence Functional Theories
Previous: Introduction, Motivation
Contents
Index
Single Path Integrals
We assume a time-independent Hamiltonian for a particle of mass 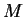 in a one-dimensional potential
in a one-dimensional potential 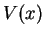 (the generalisation to larger than one dimension is easy),
(the generalisation to larger than one dimension is easy),
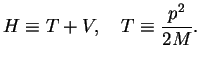 |
|
|
(153) |
The solution of the Schrödinger equation can be written as
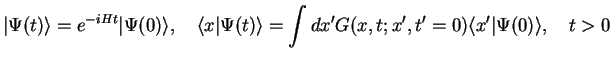 |
|
|
(154) |
with the help of the propagator
We now use the Trotter product formula
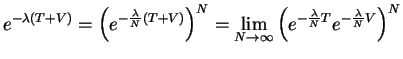 |
|
|
(156) |
with
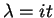 (
(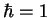 ) and write (inserting the identity
) and write (inserting the identity 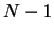 times)
times)
Now use (cf. p 1.15, 1.17),
where we analytically continued the formula
for Gaussian integrals
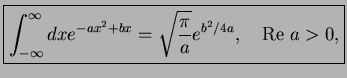 |
|
|
(159) |
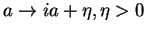 , cf. Fresnel integrals and the book by H. Kleinert, `Path Integrals' 2nd edition, World Scientific (Singapore, 1995).
, cf. Fresnel integrals and the book by H. Kleinert, `Path Integrals' 2nd edition, World Scientific (Singapore, 1995).
We now introduce
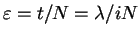 and have
and have
Here, we have defined the Lagrange Function 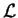 for the
path
for the
path
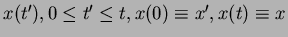 with
start point
with
start point 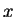 and end point
and end point 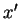 in configuration space. The Feynman path integral measure
in configuration space. The Feynman path integral measure
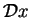 is a symbolic way of writing the limit
is a symbolic way of writing the limit
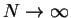 ,
,
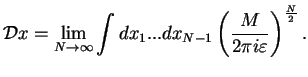 |
|
|
(161) |





Next: Double Path Integrals
Up: Feynman-Vernon Influence Functional Theories
Previous: Introduction, Motivation
Contents
Index
Tobias Brandes
2004-02-18
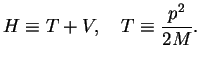
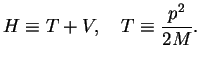
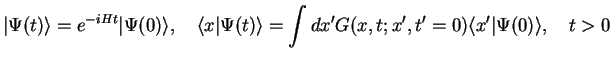
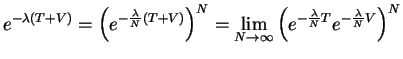
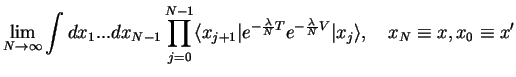
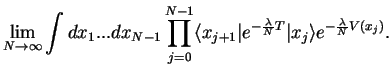
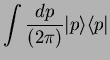
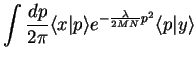
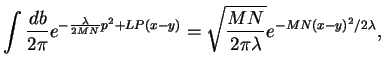
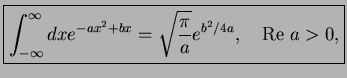
![]() and have
and have
![$\displaystyle \lim_{N\to \infty} \int dx_1...dx_{N-1} \left(\frac{MN}{2\pi \lam...
...p \left[
-\frac{MN(x_j-x_{j+1})^2}{2\lambda} - \frac{\lambda V(x_j)}{N} \right]$](img698.png)
![$\displaystyle \lim_{N\to \infty} \int dx_1...dx_{N-1} \left(\frac{M}{2\pi i \va...
...eft[ \frac{M}{2}
\frac{(x_j-x_{j+1})^2}{\varepsilon^2} - V(x_j) \right] \right]$](img699.png)