




Next: Expansion of the Influence
Up: Feynman-Vernon Influence Functional Theories
Previous: `Re-Exponentiation'
Contents
Index
`Semiclassical' Limit for Damped Single Particle Motion
References: A. Schmid, J. Low Temp. Phys. 49, 609 (1982);
W. Zwerger, Phys. Rev. B 35, 4737 (1987); N. Janssen and W. Zwerger, Phys. Rev. B 52, 9406 (1995);
U. Weiss, `Quantum Dissipative Systems' (2nd ed.), World Scientific (Singapore) (1999), ch. 5.5.
Let us assume a single particle in a potential 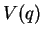 ,
,
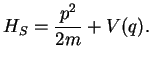 |
|
|
(223) |
We consider the reduced density matrix 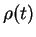 of the system
of the system 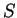 ,
,
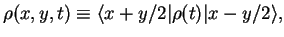 |
|
|
(224) |
where we set
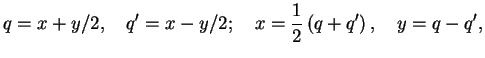 |
|
|
(225) |
thus introducing the `center-of-mass' coordinate 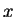 and the relative coordinate
and the relative coordinate
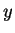 . Note that
the Wigner distribution function
. Note that
the Wigner distribution function 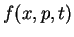 is obtained from the density matrix as
a Fourier transform with respect to the relativ co-ordinate
is obtained from the density matrix as
a Fourier transform with respect to the relativ co-ordinate 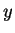 ,
,
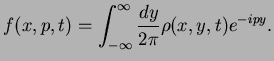 |
|
|
(226) |
Correspondingly, in the double path integral we integrate over
center-of-mass-coordinate and relative-coordinate paths,
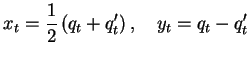 |
|
|
(227) |
The Jacobian of the corresponding discretised variable transformation is one whence one can write
Subsections





Next: Expansion of the Influence
Up: Feynman-Vernon Influence Functional Theories
Previous: `Re-Exponentiation'
Contents
Index
Tobias Brandes
2004-02-18
![]() ,
,
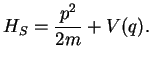
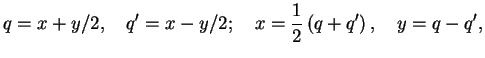
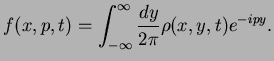
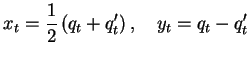
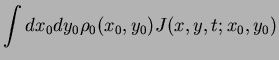
![$\displaystyle \int_{x_0}^x {\cal D}x \int_{y_0}^y{\cal D}y \exp \left[
i\int_{0}^{t}dt'\left(M\dot{x}_{t'}\dot{y}_{t'} - V(x+y/2) + V(x-y/2) \right)\right]$](img966.png)