Next: Application: Polaron-Transport
Up: `Semiclassical' Limit for Damped
Previous: Discussion
Contents
Index
The influence phase for the linear model, Eq.(7.212), the influence phase is
(cf. Eq. (7.235,7.214,7.213))
whence the deterministic friction force
![$ F_B[x_s,t']$](img1002.png) becomes
becomes
The term 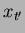 from the integration by parts has cancelled exactly with the counter-term
from the integration by parts has cancelled exactly with the counter-term
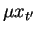 .
If one now assumes a linear spectral function
.
If one now assumes a linear spectral function 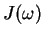 ,
,
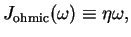 |
|
|
(252) |
we recover the original Caldeira-Leggett description of quantum friction (plus
the additional term
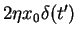 that was missing there, cf. A. O. Caldeira, A. J. Leggett,
Physica 121 A, 587 (1983); ibid. 130 A, 374(E), (1985); Weiss book chapter 5.1),
that was missing there, cf. A. O. Caldeira, A. J. Leggett,
Physica 121 A, 587 (1983); ibid. 130 A, 374(E), (1985); Weiss book chapter 5.1),
The resulting stochastic equation of motion Eq. (7.251) is
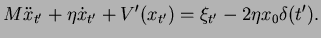 |
|
|
(254) |
Note that the `awkward' term
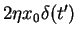 brings in a dependence on the `initial condition'
brings in a dependence on the `initial condition' 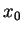 .
.





Next: Application: Polaron-Transport
Up: `Semiclassical' Limit for Damped
Previous: Discussion
Contents
Index
Tobias Brandes
2004-02-18
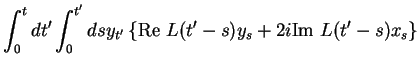
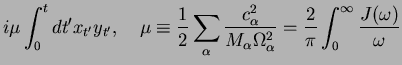
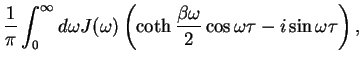
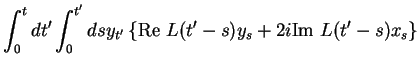
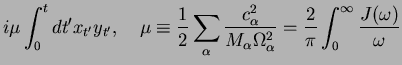
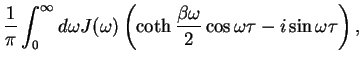
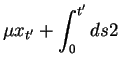 Im
Im 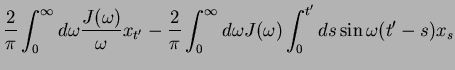
![$\displaystyle \frac{2}{\pi}\int_{0}^{\infty}d\omega\frac{J(\omega)}{\omega}x_{t...
...'}{\omega}x_0
- \int_{0}^{t'}ds\frac{\cos \omega(t'-s)}{\omega}\dot{x}_s\right]$](img1066.png)
![$\displaystyle \frac{2}{\pi}\int_{0}^{\infty}d\omega J(\omega)
\left[ \frac{\cos...
...}{\omega}x_0 + \int_{0}^{t'}ds\frac{\cos \omega(t'-s)}{\omega}\dot{x}_s\right].$](img1067.png)
![$\displaystyle \frac{2\eta}{\pi} \int_{0}^{\infty}d\omega
\left[x_0\cos \omega t'+ \int_{0}^{t'}ds\cos \omega(t'-s)\dot{x}_s\right]$](img1072.png)