




Next: Constant
Up: Time-dependent Hamiltonians
Previous: Time-dependent Hamiltonians
Contents
Index
This case is, for example, extremely important for NMR (nuclear magnetic resonance).
Even here the Hamiltonian
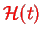 is in general not exactly soluble, its form is
is in general not exactly soluble, its form is
where the Pauli-matrices are defined as
Why is that so difficult? Let us write the Schrödinger equation
We assume
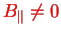 and
write (omit the
and
write (omit the
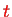 -dependence for a moment)
-dependence for a moment)
This is a second order ODE with time-dependent coefficients, which in general is not solvable in terms of known functions (it can of course be solved numerically quite easily).
Subsections





Next: Constant
Up: Time-dependent Hamiltonians
Previous: Time-dependent Hamiltonians
Contents
Index
Tobias Brandes
2005-04-26
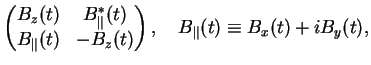
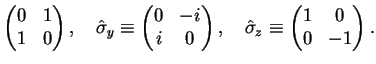
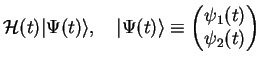
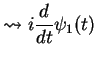
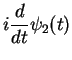
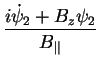
![$\displaystyle \frac{\dot{B_{\Vert}}}{B_{\Vert}} [ i\dot{\psi}_2 + B_z \psi_2] -...
...\Vert} [B_z \psi_1 + B_{\Vert}^* \psi_2]
- \dot{B_z} \psi_2 - B_{z}\dot{\psi_2}$](img1089.png)
![$\displaystyle \frac{\dot{B_{\Vert}}}{B_{\Vert}} [ i\dot{\psi}_2 + B_z \psi_2]
-...
...z \psi_2] -iB_{\Vert} B_{\Vert}^* \psi_2
- \dot{B_z} \psi_2 - B_{z}\dot{\psi_2}$](img1090.png)
![$\displaystyle i\frac{\dot{B_{\Vert}}}{B_{\Vert}} \dot{\psi}_2 + \left[ \frac{\d...
...}{B_{\Vert}} B_z
-i B_z^2 -i \vert B_{\Vert}\vert^2 - \dot{B}_z \right] \psi_2.$](img1091.png)