Coulomb Gauge

In the Coulomb gauge one sets

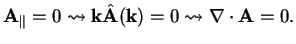$$\mathbf{A}_\Vert =0 \leadsto {\bf k}\hat{\mathbf{A}}({\bf k})=0 \leadsto \div\mathbf{A}=0.$$ (1.16)

The vector potential 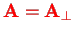$\mathbf{A}= \mathbf{A}_\perp$ is purely transverse in the Coulomb gauge. We then have

$$\hat{\mathbf{E}}({\bf k}) = -i {\bf k}\phi({\bf k}) - \partial_t\hat{\mathbf{A}}({\bf k})\leadsto$$

$${\bf k} \hat{\mathbf{E}}({\bf k}) = -i{\bf k} {\bf k}\phi({\bf k}) - \partial_t{\bf k}\hat{\mathbf{A}}({\bf k}) = -i{\bf k} {\bf k}\phi({\bf k})$$ (1.17)

$$\leadsto -i \rho({\bf k})/\varepsilon_0 = -i{\bf k} {\bf k}\phi({\bf k}) \leadsto \nabla^2 \phi({\bf r},t) = -\rho({\bf r},t)/\varepsilon_0,$$ (1.18)

which is the Poisson equation.