Next: Born-Oppenheimer Approximation
Up: Hamiltonian
Previous: Hamiltonian
Contents
Index
If two particles have positions
 and
and
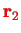 and momenta
and momenta
 and
and
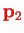 , the angular
momentum of the total system of the two particles is
, the angular
momentum of the total system of the two particles is
We introduce center-of-mass and relative coordinates according to
and furthermore momenta
Note that the relative momentum
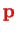 is not just the difference of the individual momenta. It is rather defined such that in terms of
is not just the difference of the individual momenta. It is rather defined such that in terms of
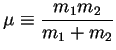 reduced mass reduced mass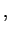 |
|
|
(1.5) |
one has
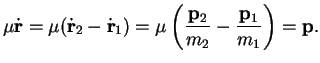 |
|
|
(1.6) |
Using these definitions, one checks
This is the sum of a center-of-mass angular momentum,
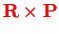 , and a relative angular momentum,
, and a relative angular momentum,
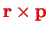 .
.





Next: Born-Oppenheimer Approximation
Up: Hamiltonian
Previous: Hamiltonian
Contents
Index
Tobias Brandes
2005-04-26
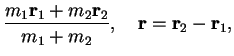
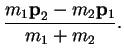
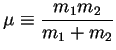 reduced mass
reduced mass