




Next: Coulomb Potential
Up: Hydrogen Atom (non-relativistic)
Previous: Hydrogen Atom (non-relativistic)
Contents
Index
The Hamiltonian for two particles of mass 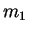 and
and 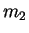 interacting via a potential
interacting via a potential 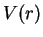 ,
,
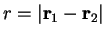 , is given by
, is given by
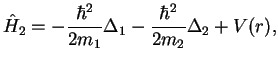 |
|
|
(1.1) |
where 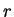 is the distance between the two particles with positions
is the distance between the two particles with positions 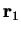 and
and 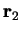 , and
, and 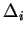 is the Laplace operator with respect to coordinate
is the Laplace operator with respect to coordinate 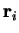 , cf. the textbook Landau-Lifshitz III [1]. This is reduced to a single particle problem by introducing
center-of-mass and relative coordinates,
, cf. the textbook Landau-Lifshitz III [1]. This is reduced to a single particle problem by introducing
center-of-mass and relative coordinates,
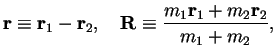 |
|
|
(1.2) |
which as in Classical Mechanics leads to a separation
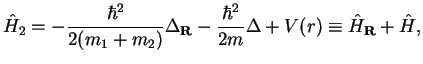 |
|
|
(1.3) |
where
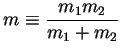 |
|
|
(1.4) |
is called reduced mass and
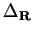 and
and 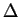 are the Laplacians with respect to
are the Laplacians with respect to 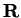 and
and 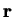 . If we write
. If we write
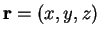 we have
we have
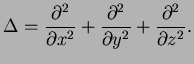 |
|
|
(1.5) |
The Hamiltonian 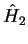 is now a sum of two independent Hamiltonians.
is now a sum of two independent Hamiltonians.
Exercise: Check Eq. (II.1.3).
Exercise: Prove that the stationary solutions of 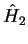 can be written in product form
can be written in product form
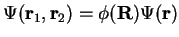 .
.





Next: Coulomb Potential
Up: Hydrogen Atom (non-relativistic)
Previous: Hydrogen Atom (non-relativistic)
Contents
Index
Tobias Brandes
2005-04-26
![]() and
and ![]() interacting via a potential
interacting via a potential ![]() ,
,
![]() , is given by
, is given by
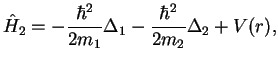
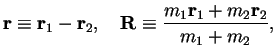
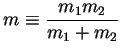
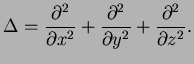
![]() can be written in product form
can be written in product form
![]() .
.