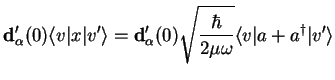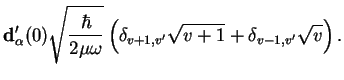Next: Vibration-Rotation Spectra
Up: Pure Vibration
Previous: Recap of the Harmonic
Contents
Index
Pure vibrational transitions are between states where only vibrational quantum numbers are changed,
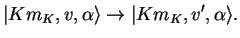 |
|
|
(2.13) |
Such transitions then depend on matrix elements of the dipole operator,
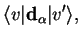 |
|
|
(2.14) |
where
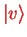 is an harmonic oscillator eigenstate (we write
is an harmonic oscillator eigenstate (we write
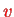 instead of
instead of
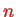 now), and
now), and
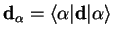 |
|
|
(2.15) |
is the diagonal matrix element of the dipole operator between the adiabatic electronic eigenstates
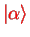 .
.
Remember that the harmonic potential came from the Taylor expansion of the Born-Oppenheimer energy,
where the harmonic oscillator coordinate
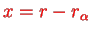 .
.
The dipole moment operator
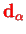 depends on the electronic wave functions
depends on the electronic wave functions
 and thus parametrically on the coordinate
and thus parametrically on the coordinate
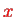 that describes the internuclear separation. We Taylor-expand
that describes the internuclear separation. We Taylor-expand
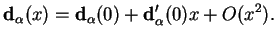 |
|
|
(2.18) |
For transitions between
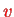 and
and
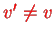 , one therefore has to linear approximation
, one therefore has to linear approximation
The vibrational selection rule thus is
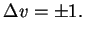 |
|
|
(2.20) |
The corresponding energy differences determine the transition frequency,
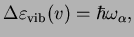 |
|
|
(2.21) |
which means that a purely vibrational, harmonic spectrum just consists of a single spectral line!





Next: Vibration-Rotation Spectra
Up: Pure Vibration
Previous: Recap of the Harmonic
Contents
Index
Tobias Brandes
2005-04-26
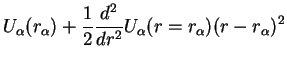
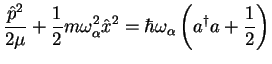
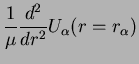
![]() depends on the electronic wave functions
depends on the electronic wave functions
![]() and thus parametrically on the coordinate
and thus parametrically on the coordinate
![]() that describes the internuclear separation. We Taylor-expand
that describes the internuclear separation. We Taylor-expand