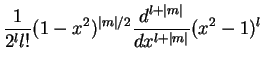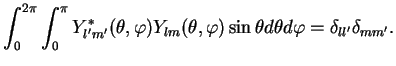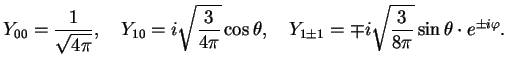Next: Radial Solutions
Up: Hydrogen Atom (non-relativistic)
Previous: Coulomb Potential
Contents
Index
The central potential has rotational symmetry and therefore a conserved quantity, the angular momentum (Nöther's theorem ![[*]](file:/usr/share/latex2html/icons/footnote.png) ). Here, we introduce polar coordinates and realise that the Laplacian can be written as
). Here, we introduce polar coordinates and realise that the Laplacian can be written as
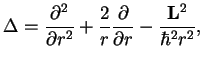 |
|
|
(1.9) |
where the angular momentum is
and its square is given by
![$\displaystyle {\bf\hat{L}}^2=
-\hbar^2 \left[\frac{1}{\sin \theta}\frac{\partia...
...a}\right)
+\frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2}\right].$](img56.png) |
|
|
(1.11) |
The eigenvalue equations for
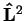 and
and 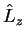 are
are
where the spherical harmonics have quantum numbers
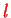 and
and
 and the explicit form
and the explicit form
The 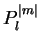 are called associated Legendre polynomials. The spherical harmonics
are an orthonormal function system on the surface of the unit sphere
are called associated Legendre polynomials. The spherical harmonics
are an orthonormal function system on the surface of the unit sphere
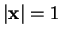 . We write
the orthonormality relation both in our abstract bra -ket and in explicit form:
. We write
the orthonormality relation both in our abstract bra -ket and in explicit form:
The spherical harmonics with
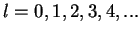 are denoted as
are denoted as
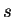 -,
-, 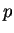 -,
-, 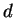 -,
-, 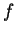 -,
-, 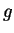 -,... functions which you might know already from chemistry (`orbitals').
The explicit forms for some of the first sphericals are
-,... functions which you might know already from chemistry (`orbitals').
The explicit forms for some of the first sphericals are
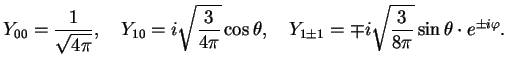 |
|
|
(1.16) |
Figure:
Absolute squares of various spherical harmonics. From http://mathworld.wolfram.com/SphericalHarmonic.html
|
|
Further information on spherical harmonics in various books and under
http://mathworld.wolfram.com/SphericalHarmonic.htmlhttp://mathworld.wolfram.com/SphericalHarmonic.html.
The Spherical harmonics are used in many areas of science, ranging from nuclear physics up to computer vision tasks. If you like online physics teaching, have a look at
http://scienceworld.wolfram.com/physics/HydrogenAtom.htmlhttp://scienceworld.wolfram.com/physics/HydrogenAtom.html .





Next: Radial Solutions
Up: Hydrogen Atom (non-relativistic)
Previous: Coulomb Potential
Contents
Index
Tobias Brandes
2005-04-26
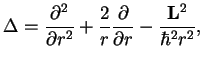
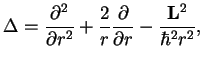
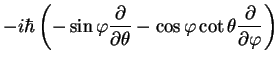
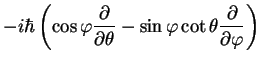
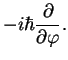
![$\displaystyle {\bf\hat{L}}^2=
-\hbar^2 \left[\frac{1}{\sin \theta}\frac{\partia...
...a}\right)
+\frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2}\right].$](img56.png)
![$\displaystyle (-1)^{(m+\vert m\vert)/2}i^l
\left[\frac{2l+1}{4\pi}\frac{(l-\ver...
...}{(l+\vert m\vert)!}\right]^{1/2}
P_l^{\vert m\vert}(\cos \theta) e^{im\varphi}$](img66.png)