![$\displaystyle \left[ \hat{H_0} + {\sum_i \int d{\bf r'} \vert\psi_{\nu_{i}}({\bf r'})\vert^2 U(\vert{r-r'}\vert)} \right]
\psi_{\nu_{j}}({\bf r})$](img709.png) |
|||
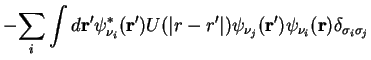 |
(4.2) |
The Hartree-Fock equations in the position representation are
a) Simplify the Hartree-Fock equations by using the orthonormality of the
![]() .
.
b) Thus solve the Hartree-Fock equations for the ground state wave function
![]() explicitly.
explicitly.
c) Using b), calculate the Hartree-Fock ground state energy
![$\displaystyle E_{\Psi}=\frac{1}{2}\sum_{i=1}^{N} \left[ \varepsilon_i+ \langle\nu_{i}\vert\hat{H}_0 \vert \nu_{i}\rangle\right].$](img1621.png) |
(4.3) |
d) Compare the Hartree-Fock ground state energy
![]() with the exact ground state energy
with the exact ground state energy
![]() from the exact solution of the previous problem and briefly discuss your result.
from the exact solution of the previous problem and briefly discuss your result.