Example: Two-Level System

Figure: Vector representation of left and right lowest states of double well potential.

The two-level system describes a particle in an `abstract' double well with just two states. We associate a Hamiltonian 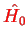$\hat{H_0}$ with the two isolated wells: the unperturbated Hamiltonian is a two-by-two matrix,

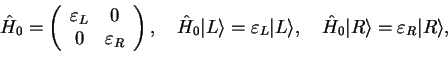$$\hat{H}_0=\left( \begin{array}{cc} \varepsilon_L & 0\\ 0 & \... ... \quad \hat{H}_0 \vert R\rangle = \varepsilon_R \vert R\rangle,$$ (2.2)

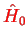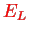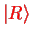i.e., $\vert L\rangle$ is eigenvector of $\hat{H}_0$ with eigenvalue $E_L$ and $\vert R\rangle$ is eigenvector with eigenvalue 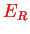$E_R$. The tunnel effect is considered as a perturbation 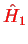$\hat{H}_1$ to $\hat{H}_0$,

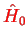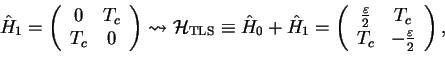$$\hat{H}_1= \left( \begin{array}{cc} 0 & T_c\\ T_c & 0 \end{a... ...n}{2} & T_c\\ T_c & -\frac{\varepsilon}{2} \end{array}\right),$$ (2.3)

with a tunnel coupling 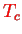$T_c$ (real parameter). We furthermore set 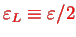$\varepsilon_L\equiv \varepsilon/2$ and $\varepsilon_R = -\varepsilon/2$.