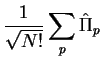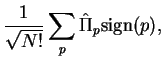Next: -Boson systems
Up: Basis vectors for Fermi
Previous: -particle system
Contents
Index
There are
 permutations of
permutations of
 particles. We label the permutations by
particles. We label the permutations by
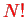 indices
indices
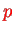 and define a permutation operator
and define a permutation operator
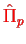 , for example
, for example
We furthermore define the symmetrization operator
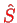 and the anti-symmetrization operator
and the anti-symmetrization operator
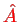 ,
,
where
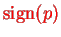 is the sign of the permutation which is either
is the sign of the permutation which is either
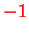 or
or
 ,
,
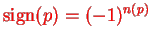 where
where
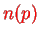 is the number of swaps required to achieve the permutation
is the number of swaps required to achieve the permutation
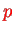 .
.





Next: -Boson systems
Up: Basis vectors for Fermi
Previous: -particle system
Contents
Index
Tobias Brandes
2005-04-26