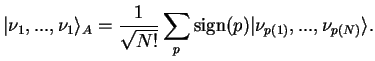Next: 2-Fermion Systems
Up: Basis vectors for Fermi
Previous: -Boson systems
Contents
Index
In this case, we have to use anti-symmetrized states with anti-symmetric wave functions,
These determinants are called Slater determinants.
- A permutation of two of the particles here corresponds to a swapping of the corresponding columns in the determinant and therefore gives a minus sign: the wave function is anti-symmetric.
- If two of the quantum numbers
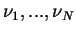 are the same, the determinant is zero: in a system with identical Fermions, two or more than two particles can not be in the same state (in contrast to Bosons). This important fact is called Pauli principle.
are the same, the determinant is zero: in a system with identical Fermions, two or more than two particles can not be in the same state (in contrast to Bosons). This important fact is called Pauli principle.
Finally, we remark that in Slater determinants we can let the permutations all operate either on the coordinates
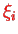 , or all on the indices
, or all on the indices
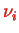 :
:
Exercise: Explicitly verify this identity for the case of
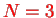 particles.
particles.
This is in particular useful when it comes to calculation of matrix elements. The last form
justifies the notation
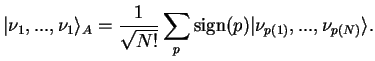 |
|
|
(1.26) |





Next: 2-Fermion Systems
Up: Basis vectors for Fermi
Previous: -Boson systems
Contents
Index
Tobias Brandes
2005-04-26
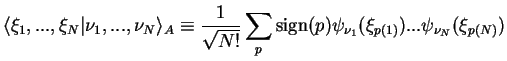
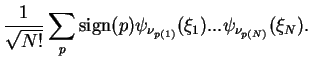
![]() particles.
particles.