




Next: The Variational Principle for
Up: The Variational Principle
Previous: Functional Derivates
Contents
Index
The additional condition
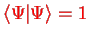 can be incorporated into the minimisation procedure by
adding a term to the energy functional, introducing a Lagrange multiplier
can be incorporated into the minimisation procedure by
adding a term to the energy functional, introducing a Lagrange multiplier
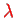 , and thereby defining the functional
, and thereby defining the functional
![$\displaystyle F[\Psi] \equiv E[\Psi] + \lambda \left[\langle \Psi \vert \Psi \rangle-1\right].$](img651.png) |
|
|
(3.8) |
Its functional derivative is
Exercise: Check this equation.
Minimization then means
![$\displaystyle 0= \frac{\delta F[\Psi]}{\delta \Psi}\leadsto \langle \delta \Psi...
... \Psi \rangle +
\langle \Psi\vert \hat{H}+\lambda\vert \delta \Psi \rangle = 0.$](img654.png) |
|
|
(3.10) |
As
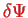 is arbitrary and complex, this can only be true if
is arbitrary and complex, this can only be true if
![$\displaystyle [\hat{H}+\lambda]\vert \Psi \rangle =0,\quad \langle \Psi\vert [\hat{H}+\lambda]=0$](img655.png) |
|
|
(3.11) |
which are two equations which are the conjugate complex to each other. Writing
 , this means
, this means
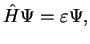 |
|
|
(3.12) |
which is the stationary Schrödinger equation. However, here
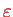 is the lowest eigenvalue with corresponding eigenstate
is the lowest eigenvalue with corresponding eigenstate
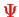 . We thus recognise:
. We thus recognise:
Minimization of the functional
![\bgroup\color{col1}$ F[\Psi] \equiv E[\Psi] -\varepsilon \left[\langle \Psi \vert \Psi \rangle-1\right]$\egroup](img658.png) is equivalent to finding the lowest eigenvalue and eigenstate of the stationary Schrödinger equation
is equivalent to finding the lowest eigenvalue and eigenstate of the stationary Schrödinger equation
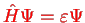 .
.





Next: The Variational Principle for
Up: The Variational Principle
Previous: Functional Derivates
Contents
Index
Tobias Brandes
2005-04-26
![$\displaystyle \frac{\delta F[\Psi]}{\delta \Psi}$](img652.png)
![$\displaystyle 0= \frac{\delta F[\Psi]}{\delta \Psi}\leadsto \langle \delta \Psi...
... \Psi \rangle +
\langle \Psi\vert \hat{H}+\lambda\vert \delta \Psi \rangle = 0.$](img654.png)
![]() is equivalent to finding the lowest eigenvalue and eigenstate of the stationary Schrödinger equation
is equivalent to finding the lowest eigenvalue and eigenstate of the stationary Schrödinger equation
![]() .
.