




Next: Hartree-Fock for Molecules
Up: Bonding and Antibonding
Previous: Symmetries of MOs in
Contents
Index
Within BO approximation, the energies
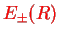 enter the nuclear Hamiltonian (cf. Eq. (
enter the nuclear Hamiltonian (cf. Eq. (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) with
) with
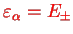 ) for the wave functions
) for the wave functions
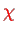
of the nuclear system with
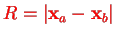 , cf. Eq. (V.3.1).
Clearly, a separation in center-of mass and relative motion is easily done here. The potential energy for the nuclei is given by the function
, cf. Eq. (V.3.1).
Clearly, a separation in center-of mass and relative motion is easily done here. The potential energy for the nuclei is given by the function
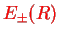 , cf.
Eq. (V.3.22),
, cf.
Eq. (V.3.22),
![$\displaystyle E_{\pm}(R)= E_{1s}+\frac{e^2}{4\pi\varepsilon_0 a_0}\left[\frac{1}{R}\mp \frac{j(R)\pm k(R)}{1\pm S(R)}\right],$](img937.png) |
|
|
(3.26) |
with the explicit expression for
 ,
,
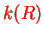 ,
,
 , in Eq. (V.3.22). The parametric eigenenergies of the electronic system become the potential for the nuclei, which is the characteristic feature of the BO approximation. The corresponding potential curves are shown in Fig.(V.3.3.4).
, in Eq. (V.3.22). The parametric eigenenergies of the electronic system become the potential for the nuclei, which is the characteristic feature of the BO approximation. The corresponding potential curves are shown in Fig.(V.3.3.4).
Figure:
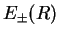 , Eq. (V.3.26), for the
, Eq. (V.3.26), for the 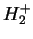 -ion in Born-Oppenheimer approximation and using the MO-LCAO Rayleigh-Ritz method, from Weissbluth [4].
-ion in Born-Oppenheimer approximation and using the MO-LCAO Rayleigh-Ritz method, from Weissbluth [4].
|
|
- The potential energy
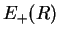 of the bonding molecular orbital has a minimum at
of the bonding molecular orbital has a minimum at 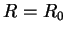 . This determines the equilibrium position of the two nuclei. Occupation of the bonding MO helps to bond the nuclei together and thereby form the molecule.
. This determines the equilibrium position of the two nuclei. Occupation of the bonding MO helps to bond the nuclei together and thereby form the molecule.
- The potential energy
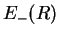 of the antibonding molecular orbital has no local minimum. Therefore, the antibonding state is an excited state in which the molecule dissociates.
of the antibonding molecular orbital has no local minimum. Therefore, the antibonding state is an excited state in which the molecule dissociates.





Next: Hartree-Fock for Molecules
Up: Bonding and Antibonding
Previous: Symmetries of MOs in
Contents
Index
Tobias Brandes
2005-04-26
![$\displaystyle \left[ \sum_{i=a,b}\frac{{\bf P}_i^2}{2M}
+ E_{\pm}(R)\right]\chi_{\pm}({\bf x}_a,{\bf x}_b)$](img934.png)
![$\displaystyle \left[ \sum_{i=a,b}\frac{{\bf P}_i^2}{2M}
+ E_{\pm}(R)\right]\chi_{\pm}({\bf x}_a,{\bf x}_b)$](img934.png)
![\includegraphics[width=1\textwidth]{energy_H2}](img941.png)