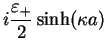Next: Case
Up: A more complicated case
Previous: Case of no potential
Contents
For a rectangular tunnel barrier of width 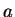 and height
and height 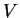 , that is
, that is
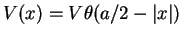 , we have calculated
the transfer matrix
, we have calculated
the transfer matrix 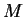 before (note that now the width is
before (note that now the width is 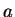 and not
and not 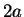 ,
,
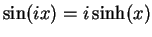 , and
, and
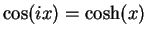 :
:
From this and Eq. (2.76), we obtain
We multiply this equation by
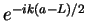 and take the real part to
obtain two equations for the even and the odd case. We can check that taking the imaginary part
leads to the same result. Using
and take the real part to
obtain two equations for the even and the odd case. We can check that taking the imaginary part
leads to the same result. Using
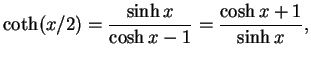 |
|
|
(156) |
we obtain
Subsections




Next: Case
Up: A more complicated case
Previous: Case of no potential
Contents
Tobias Brandes
2004-02-04
![$\displaystyle e^{ika}\left[\cosh (\kappa a) +i\frac{\varepsilon_-}{2}\sinh (\kappa a)\right ]$](img661.png)