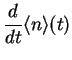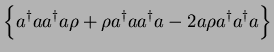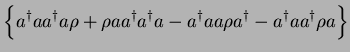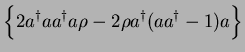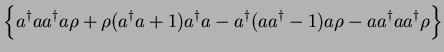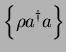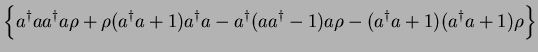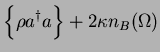Next: Master Equation (Non-RWA Model)
Up: Master Equation II: the
Previous: Final Form of Master
Contents
Index
We would like to use our Master equation Eq.(7.48)
and calculate some `useful' quantities as, for examples, expectation values
of System ( oscillator) observables
oscillator) observables
 . Let us do this for the
number operator,
. Let us do this for the
number operator,
 . Multiplying with
. Multiplying with  and taking the trace, we obtain
and taking the trace, we obtain
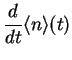 |
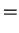 |
 Tr Tr![$\displaystyle \left( n[a^{\dagger}a,{\rho}]\right)
- \kappa$](img205.png) Tr Tr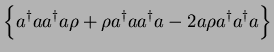 |
|
| |
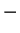 |
 Tr Tr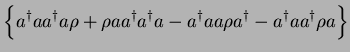 |
|
| |
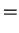 |
 Tr Tr Tr Tr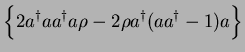 |
|
| |
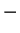 |
 Tr Tr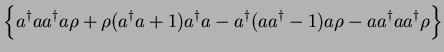 |
|
| |
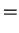 |
 Tr Tr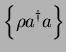 |
|
| |
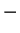 |
 Tr Tr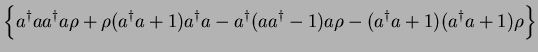 |
|
| |
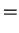 |
 Tr Tr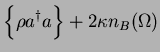 |
|
| |
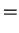 |
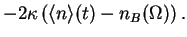 |
(50) |
This now is a simple first order differential equation which has the solution
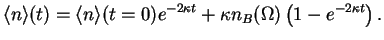 |
|
|
(51) |
In particular, one has
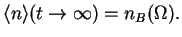 |
|
|
(52) |
For large times, the occupation number is thus given by the thermal equilibrium Bose distribution,
regardless of the initial condition
 .
.





Next: Master Equation (Non-RWA Model)
Up: Master Equation II: the
Previous: Final Form of Master
Contents
Index
Tobias Brandes
2004-02-18

![$\displaystyle -i\bar{\Omega}[a^{\dagger}a,{\rho}]
- \kappa \Big\{ a^{\dagger} a {\rho} + \rho a^{\dagger} a - 2 a \rho a^{\dagger}
\Big\}$](img197.png)


![$\displaystyle -i\bar{\Omega}[a^{\dagger}a,{\rho}]
- \kappa \Big\{ a^{\dagger} a {\rho} + \rho a^{\dagger} a - 2 a \rho a^{\dagger}
\Big\}$](img197.png)