




Next: Properties of
Up: Thermal Bath Correlation Function
Previous: Definition
Contents
Index
All the dependence on the coupling constants  is encapsulated within the
spectral density
is encapsulated within the
spectral density
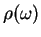 .
The latter is often parametrised as
.
The latter is often parametrised as
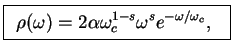 |
|
|
(54) |
where  is the dimensionless coupling parameter and
is the dimensionless coupling parameter and  is the cutoff frequency.
Note that
is the cutoff frequency.
Note that
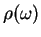 has the dimension
has the dimension ![$ [\omega]$](img228.png) which is the reason for the
pre-factor
which is the reason for the
pre-factor
 . The parameter
. The parameter  determines the low-frequency behaviour of
determines the low-frequency behaviour of
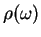 , and one calls couplings with
, and one calls couplings with
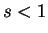 |
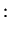 |
sub-ohmic |
|
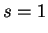 |
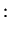 |
ohmic |
|
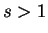 |
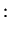 |
super-ohmic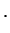 |
(55) |
This classification has its origin in the analysis of the dissipative two-level
(spin-boson) system which we will discuss below.
The case

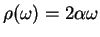 |
|
|
(56) |
is called scaling limit of the ohmic bath and has the special property of homogeneity
 .
.





Next: Properties of
Up: Thermal Bath Correlation Function
Previous: Definition
Contents
Index
Tobias Brandes
2004-02-18
![]()