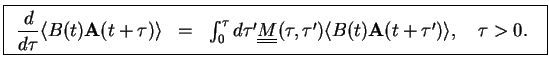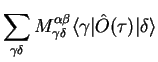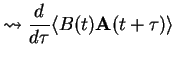Next: The Two-Level System I
Up: Correlation Functions and the
Previous: Correlation Functions and the
Contents
Index
Correlation functions are important since they can tell us a lot
about the dynamics of dissipative systems. Moreover, they are often directly related to
experimentally accessible quantities, such as photon or electron noise. In quantum
optics, fluctuations of the photon field are expressed by correlations functions
such as
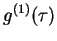 and
and
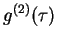 .
.
We would like to calculate the correlation function of two system operators 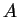 and
and 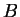 ,
,
 |
|
|
(98) |
We insert the time evolution of the operators,
to find
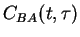 |
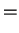 |
Tr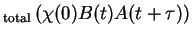 |
|
| |
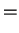 |
Tr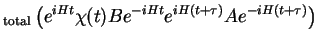 |
|
| |
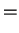 |
Tr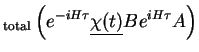 |
|
| |
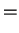 |
Tr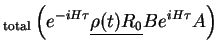 Born Approximation Born Approximation |
|
| |
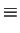 |
Tr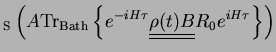 |
|
| |
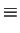 |
Tr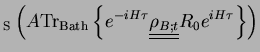 |
|
| |
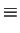 |
Tr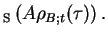 |
(99) |
The correlation function can therefore be written as
an expectation value of 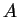 with a `modified system density matrix'
with a `modified system density matrix'
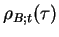 which starts at
which starts at 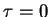 as
as
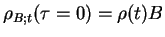 and evolves as a function of time
and evolves as a function of time 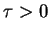 .
.
For the time-evolution of a system operator 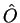 according to
according to
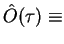 Tr Tr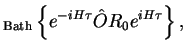 |
|
|
(100) |
we can write a formal operator equation
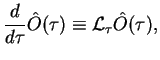 |
|
|
(101) |
where we introduced the super-operator
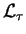 .
.
Example: Master equation for
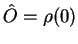 in Born and Markov approximation, cf. Eq.(7.33)
in Born and Markov approximation, cf. Eq.(7.33)
It is important to realise that
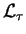 is a linear operator.
We now assume that the system has a basis of kets
is a linear operator.
We now assume that the system has a basis of kets
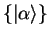 and
express the linearity of
and
express the linearity of
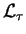 by writing the matrix elements of
by writing the matrix elements of
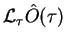 ,
,
with a time-dependent memory kernel as a
fourth-order tensor
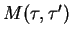 that relates
the matrix elements of the system operator
that relates
the matrix elements of the system operator 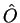 at earlier times to
its matrix elements of the (time-evolved) system operator at later times.
at earlier times to
its matrix elements of the (time-evolved) system operator at later times.
Using now
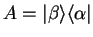 in
in 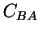 , we have
, we have
Introducing
we convert the tensor equation into a vector equation,
which can be written in compact form using the vector of operators,
![$\displaystyle {\bf A} \equiv \left(\begin{array}[h]{c} A_1 \\ A_2 \\ .. \\ A_k\\ .. \end{array}\right).$](img492.png) |
|
|
(106) |
In vector and matrix notation, we thus obtain the
quantum regression theorem ,
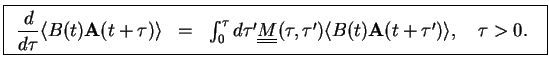 |
|
|
(107) |
Remarks:





Next: The Two-Level System I
Up: Correlation Functions and the
Previous: Correlation Functions and the
Contents
Index
Tobias Brandes
2004-02-18
![]() and
and ![]() ,
,

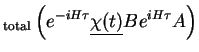
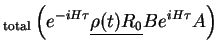 Born Approximation
Born Approximation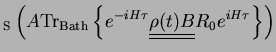
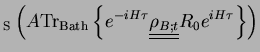
![]() according to
according to
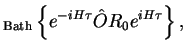
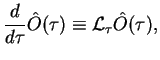
![]() in Born and Markov approximation, cf. Eq.(7.33)
in Born and Markov approximation, cf. Eq.(7.33)
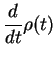
![$\displaystyle \sum_{k}\Big[
{S}_k D_k {\rho}(t) - D_k {\rho}(t)
{S}_k+
{\rho}(t)E_k {S}_k - {S}_k{\rho}(t)
E_k \Big].$](img472.png)
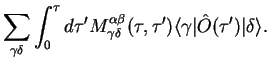
![]() in
in ![]() , we have
, we have
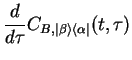
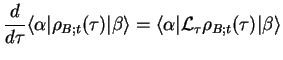
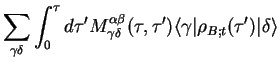
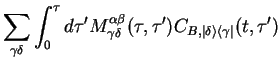
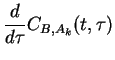
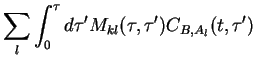
![$\displaystyle {\bf A} \equiv \left(\begin{array}[h]{c} A_1 \\ A_2 \\ .. \\ A_k\\ .. \end{array}\right).$](img492.png)