Model for $H_{SB}$: Two-Level System Coupled to Photon Bath in RWA

The microscopic interaction between a two-level atom and a photon bath is via a coupling

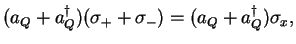$$(a_Q + a_Q^{\dagger}) ( \sigma_+ +\sigma_-)= (a_Q + a_Q^{\dagger})\sigma_x,$$ (122)

cf. Walls/Milburn, Carmichael, Baym or other quantum optics (quantum mechanics) books. Comparing with our generic form Eq.(7.114),

$$H_{SB}(t)\equiv \hat{\bf A}(t) \vec{\sigma}\equiv \sum_Q \left( {\bf g}_Q(t) a_Q^{\dagger} + {\bf g}_Q^{\dagger}(t) a_Q\right)\vec{\sigma},$$

this case would correspond to a (time-independent) coupling vector ${\bf g}_Q(t)={\bf g}_Q^{\dagger}(t)=(g_Q,0,0)$. Within the RWA, this interaction is further simplified by neglecting the `counter-rotating' terms and by writing

$${\bf g}_Q = \frac{1}{2}\gamma_Q\left( \begin{array}[h]{c} 1\\ -i \\ 0 \end{array}\right), \gamma_Q \mbox{\rm real.}$$ (123)

Assuming a free photon bath, the total Hamiltonian then is

$$H_{\rm total} \equiv H_S+H_{SB}+H_B$$

$$= H_S+ \sum_Q\gamma_Q(a_Q \sigma_+ +a_Q^{\dagger}\sigma_- ) + \sum_Q \omega_Q a_Q^{\dagger} a_Q.$$ (124)