`Monte Carlo' Procedure

Next: Feynman-Vernon Influence Functional Theories Up: Unravelling and Decomposition into Previous: Decomposition into Histories Contents Index

`Monte Carlo' Procedure

The decomposition of histories can now be simulated on a computer in order to actually solve the Master equation. Here, we only describe the simplest version (spontaneous emission, no driving field), starting from a pure state $\vert\Psi\rangle$ of the total system. For more details, see Carmichael or Plenio/Knight.

Step 1: Fix a time step $\Delta t$ . Calculate the probability $\Delta P$ of photon emission;

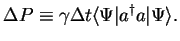$\displaystyle \Delta P \equiv \gamma \Delta t \langle \Psi \vert a^{\dagger} a \vert \Psi \rangle.$

(147)

Step 2: Compare $\Delta P$ with a random number $0 \le r \le 1$

For $\Delta P > r$ : `emission', replace

$\displaystyle \vert\Psi\rangle \to \frac{a \vert\Psi\rangle}{\Vert a \vert\Psi\rangle \Vert}$ (148)
For $\Delta P \le r$ : no emission but time-evolution under effective Hamiltonian $H_{\rm eff}$ ,

$\displaystyle \vert\Psi\rangle \to \frac{(1-i\Delta t H_{\rm eff})\vert\Psi\rangle }{(1-\Delta P)^{1/2}}$ (149)

Step 3: Go back to Step 1.

This procedure (performed with small time-steps $\Delta t$ up to a final time $t_{\rm final}$ ) yields a `curve' of simulated states $\vert\Psi(t)\rangle$ , $t\in [0,t_{\rm final}]$ in the system Hilbert space ${\cal H}_S$ . The procedure is then repeated many times in order to obtain time-dependent averages $\langle \Psi\vert \hat{\theta} \vert \Psi \rangle$ of observables $\hat{\theta}$ .

The entire procedure yields a density operator $\rho(t)=\vert\Psi\rangle \langle \Psi \vert$ that solves the original Master equation, Eq.(7.143): in one time step $\Delta t$ , we have

$\displaystyle \rho (t+\Delta t)$	$\displaystyle =$	$\displaystyle \Delta P \frac{a \vert\Psi(t)\rangle \langle \Psi (t)\vert a^{\da... ...ert (1+i\Delta t H_{\rm eff}^{\dagger}) }{(1-\Delta P)^{1/2}(1-\Delta P)^{1/2}}$
	$\displaystyle =$	$\displaystyle \gamma \Delta t a \rho(t) a^{\dagger}+ \rho(t) -i \Delta t [H,\rh... ...a t \left( a^{\dagger} a \rho(t) + \rho(t)a^{\dagger} a \right) + O(\Delta t)^2$
$\displaystyle \leadsto \frac{d}{dt}\rho(t)$	$\displaystyle =$	$\displaystyle -i [H,\rho(t)] - \kappa \Big\{ a^{\dagger} a {\rho} + \rho a^{\dagger} a - 2 a \rho a^{\dagger} \Big\} .$	(150)

Remarks:

The splitting of ${\cal L}$ as ${\cal L}={\cal L}_0+{\cal L}_1$ is not unique, there are ususally several ways of how to `unravel' the Master equation.
For more complicated Master equations, one has to extend and modify the above procedure.

Next: Feynman-Vernon Influence Functional Theories Up: Unravelling and Decomposition into Previous: Decomposition into Histories Contents Index

Tobias Brandes 2004-02-18