Double Path Integrals

Now let us come back to our density operator for our system-bath Hamiltonian,

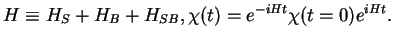$$H \equiv H_S+H_B+ H_{SB}, \chi(t)= e^{-iHt} \chi(t=0) e^{iHt}.$$ (164)

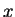For the moment, let us assume that the system has one degree of freedom $q$ and the bath the degree of freedom $x$ (the generalisation to many bath degrees of freedom $x_i$ is straightforward). We then use a representation of $\chi(t)$ in spatial coordinates,

$$\langle x,q \vert \chi(t) \vert q',x'\rangle = \int dq_0dq_0' dx_0 dx_0' \langle x,q \vert e^{-iHt}\vert q_0,x_0 \rangle \langle x_0 q_0 \vert\chi(t=0) \vert q'_0,x'_0 \rangle$$

$$\times \langle x'_0 q'_0 \vert e^{iHt} \vert q',x'\rangle.$$ (165)

We trace out the bath degree of freedoms to obtain an effective density matrix

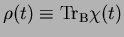$$\rho(t) \equiv {\rm Tr_B} \chi(t)$$ (166)

of the system,

$$\langle q \vert \rho(t) \vert q'\rangle = \int dq_0dq_0' dx_0 dx_0' dx \langle x,q \vert e^{-iHt}\vert q_0,x_0 \rangle \langle x_0 q_0 \vert\chi(t=0) \vert q'_0,x'_0 \rangle$$

$$\times \langle x'_0 q'_0 \vert e^{iHt} \vert q',x\rangle.$$ (167)

Now we realise that the Hamiltonian $H \equiv H_S+H_B+ H_{SB}$ induces a classical action $S_{\rm total} \equiv S_S[q]+S_B[x]+S_{SB}[xq]$, where in the following for notational simplicity we omit indices at the three $S$. We use the path integral representation for the propagator matrix elements,

$$\langle q \vert \rho(t) \vert q'\rangle = \int dq_0dq_0' dx_0 dx_0' dx \int_{q_0}^{q} {\cal{D}}q \int_{x_0}^{x} {\cal{D}}x \int_{q_0'}^{q'} {\cal{D}^*}q' \int_{x_0'}^{x'=x} {\cal{D}^*}x'$$

$$\times \exp\left[ i \left(S[q]+S[x]+S[xq]\right)-i \left(S[q']+S[x']+S[x'q']\right) \right]$$

$$\times \langle x_0 q_0 \vert\chi(t=0) \vert q'_0,x'_0 \rangle$$

$$= \int dq_0dq_0' \int_{q_0}^{q} {\cal{D}}q \int_{q_0'}^{q'} {\cal{D}^*}q' \exp\left[ i \left(S[q] - S[q']\right)\right]$$

$$\times \int dx_0 dx_0' dx \int_{x_0}^{x} {\cal{D}}x \int_{x_0'}^{x} {\ca... ...^*}x' \exp\left[ i \left(S[x]+S[xq]\right)-i \left(S[x']+S[x'q']\right) \right]$$

$$\times \langle x_0 q_0 \vert\chi(t=0) \vert q'_0,x'_0 \rangle$$

$$= [ \chi(t=0) = \rho(0) \otimes \rho_B ]$$

$$= \int dq_0dq_0' \langle q_0 \vert\rho(0)\vert q_0'\rangle \int_{q_... ...exp\left[ i \left(S[q] - S[q']\right)\right] \underline{{\cal F}[q(t'),q'(t')]}$$

$${\cal F}[q(t'),q'(t')] \equiv \int dx_0 dx_0' dx \langle x_0 \vert\rho_B\vert x_0'\rangle$$

$$\times \int_{x_0}^{x} {\cal{D}}x \int_{x_0'}^{x} {\cal{D}^*}x' \exp\left[ i \left(S[x]+S[xq]\right)-i \left(S[x']+S[x'q']\right) \right]$$

• In the original Feynman-Vernon method, one assumes a factorising initial condition $\chi(t=0) = \rho(0) \otimes \rho_B$, although that can be generalised to non-factorising initial density matrices $\chi(t=0)$, cf. for example H. Grabert, P. Schramm, G. L. Ingold, Phys. Rep. 168, 115 (1988), or the book by Weiss.
• The functional ${\cal F}[q(t'),q'(t')]$ is called influence functional . It describes the effect of the bath on the time-evolution of the system density matrix.
• For zero system-bath coupling $H_{SB}=0$, ${\cal F}[q(t'),q'(t')]=1$