




Next: Time-dependent Hamiltonians
Up: Example: Two-Level System
Previous: Eigenvectors
Contents
Index
Quantum Oscillations in Two-Level Systems
We can now easily calculate these: use an initial condition
Check out a few examples:
 (particle initially in left well): in this case, the probabilities for the particle to be in the left (right) well at time
(particle initially in left well): in this case, the probabilities for the particle to be in the left (right) well at time
 are
are
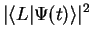 |
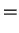 |
![$\displaystyle \cos ^2[(t-t_0)T_c]$](img1066.png) |
(1.18) |
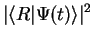 |
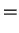 |
![$\displaystyle \sin ^2[(t-t_0)T_c]$](img1068.png) quantum-mechanical oscillations quantum-mechanical oscillations |
|





Next: Time-dependent Hamiltonians
Up: Example: Two-Level System
Previous: Eigenvectors
Contents
Index
Tobias Brandes
2005-04-26


![]() (particle initially in left well): in this case, the probabilities for the particle to be in the left (right) well at time
(particle initially in left well): in this case, the probabilities for the particle to be in the left (right) well at time
![]() are
are