Successive Interation

We can obtain the time-evolution operator $\tilde{U}(t,t_0)$ in the interaction picture by successive iteration:

$$i\partial_t \tilde{U}(t,t_0) = \tilde{V}(t) \tilde{U}(t,t_0)$$ (3.25)

$$\leadsto \tilde{U}(t,t_0) = 1-i \int_{t_0}^t dt_1 \tilde{V}(t_1) \tilde{U}(t_1,t_0)$$

$$= 1-i \int_{t_0}^t dt_1 \tilde{V}(t_1) + (-i)^2 \int_{t_0}^t dt_1 \int_{t_0}^{t_1} dt_2 \tilde{V}(t_1) \tilde{V}(t_2)+...$$

$$= 1 + \sum_{n=1}^{\infty} (-i)^n \int_{t_0}^t dt_1 \int_{t_0}^{t_1} dt_2 ...\int_{t_0}^{t_{n-1}} dt_n \tilde{V}(t_1)...\tilde{V}(t_n).$$

There is a compact notation that slightly simplifies things here: time-ordered products of operators are defined with the time-ordering operator 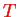$T$ which orders a product of operators $\tilde{V}(t_1)...\tilde{V}(t_n)$ with arbitrary times $t_1$,..., $t_n$ such that the `earliest' operator is left and the `latest' operator is right. For example,

$$T[ \tilde{V}(t_1)\tilde{V}(t_2)] = \theta(t_1-t_2) \tilde{V}(t_1)\tilde{V}(t_2) + \theta(t_2-t_1) \tilde{V}(t_2)\tilde{V}(t_1),$$ (3.26)

where

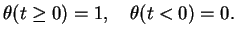$$\theta(t\ge 0)=1,\quad \theta(t< 0) = 0.$$ (3.27)

Using the time-ordering operator, one can then show

$$\tilde{U}(t,t_0) = 1 + \sum_{n=1}^{\infty} \frac{(-i)^n}{n!} \int_{t_0}^t dt_1 \int_{t_0}^{t} dt_2 ...\int_{t_0}^{t} dt_nT[\tilde{V}(t_1)...\tilde{V}(t_n)]$$

$$\equiv T \exp \left[-i \int_{t_0}^t dt' \tilde{V}(t') \right].$$ (3.28)

Note that now the upper limit of all integrals is the same $t$ and that there is the additional $1/n!$ in front of each term.