




Next: Remark on Dipole-Dipole Interaction
Up: Effective Potentials
Previous: Effective Potentials
Contents
Index
This is the simplest case: each of the
 subsystems (molecules) is considered as a distribution of charges with charge density
subsystems (molecules) is considered as a distribution of charges with charge density
 . The total charging energy is
. The total charging energy is
We assume the molecules well separated with their center of mass at
 . We first consider the contribution from two different molecules,
. We first consider the contribution from two different molecules,
 , and thus write
, and thus write
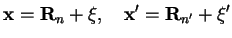 |
|
|
(2.2) |
and expand
 for each pair
for each pair
 , using the Taylor expansion
, using the Taylor expansion
with
 and
and
 .
We assume uncharged molecules, i.e.
.
We assume uncharged molecules, i.e.
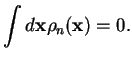 |
|
|
(2.4) |
This yields
Here, the dipole moments are defined as
and the remaining terms are dipole-quadrupole, quadrupole-quadrupole etc interaction energies which decay faster with increasing
 . Usually the dipole-dipole interaction terms are dominant over the higher multipoles for the interaction between molecules.
. Usually the dipole-dipole interaction terms are dominant over the higher multipoles for the interaction between molecules.
Summarizing, we have
Exercise: Derive the expression for

Subsections





Next: Remark on Dipole-Dipole Interaction
Up: Effective Potentials
Previous: Effective Potentials
Contents
Index
Tobias Brandes
2005-04-26





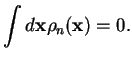

![$\displaystyle \int \int d{\bf\xi}d{\bf\xi}'\rho_n({\bf\xi})\rho_{n'}({\bf\xi}')
\frac{1}{R}\big(1 - \frac{1}{2R^2}([{\bf\xi-\xi'}]^2+ 2 {\bf R}[{\bf\xi-\xi'}])$](img1518.png)
![$\displaystyle \frac{3}{8R^4}([{\bf\xi-\xi'}]^2+ 2 {\bf R}[{\bf\xi-\xi'}])^2 + ...\big)$](img1519.png)
![$\displaystyle \int \int d{\bf\xi}d{\bf\xi}'\rho_n({\bf\xi})\rho_{n'}({\bf\xi}')...
... \frac{3}{8R^4} 4 ({\bf R}[{\bf\xi-\xi'}] )
({\bf R}[{\bf\xi-\xi'}] )+ ...\big)$](img1520.png)






![]()