.

a) Consider symmetric and anti-symmetric orbital wave functions for two Fermions,

$$\phi_{\alpha\beta}^{\pm}({\bf r}_1,{\bf r}_2) = \frac{1}{\sqrt{2}}\left[\phi_{\alpha}({\bf r}_1) \phi_{\beta}({\bf r}_2) \pm \phi_{\alpha}({\bf r}_2) \phi_{\beta}({\bf r}_1) \right],$$ (3.3)

and show that the matrix elements

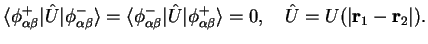$$\langle \phi_{\alpha\beta}^{+} \vert \hat{U} \vert \phi_{\alpha\b... ...hi_{\alpha\beta}^{+} \rangle=0, \quad \hat{U}=U(\vert{\bf r}_1-{\bf r}_2\vert).$$ (3.4)

b) Write down the terms

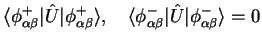$$\langle \phi_{\alpha\beta}^{+} \vert \hat{U} \vert \phi_{\alpha\b... ...gle \phi_{\alpha\beta}^{-} \vert \hat{U} \vert \phi_{\alpha\beta}^{-} \rangle=0$$ (3.5)

explicitely as double integrals. Which one is the direct term, which one is the exchange term?

c) Write down the first order correction of the ground state energy of Helium explicitely as double integrals (you don't need to calculate these integrals).