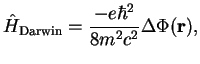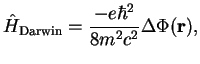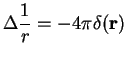Next: Spin-Orbit Coupling
Up: Kinetic Energy and Darwin
Previous: Kinetic Energy Correction
Contents
Index
This follows from the Dirac equation and is given by
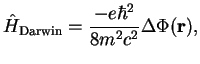 |
|
|
(3.4) |
where
 is the Laplacian. For the Coulomb potential
is the Laplacian. For the Coulomb potential
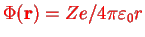 one needs
one needs
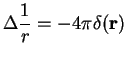 |
|
|
(3.5) |
with the Dirac Delta function
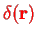 in three dimensions.
in three dimensions.
Tobias Brandes
2005-04-26