




Next: Perturbation Theory for Fine
Up: Spin-Orbit Coupling
Previous: Spin-Orbit Coupling in Atoms
Contents
Index
In solids, the spin-orbit coupling effect has shot to prominence recently in the context of
spin-electronics and the attempts to build a spin-transistor. The spin-orbit coupling
Eq. (II.3.6),
![$\displaystyle {\color{col1}\hat{H}_{\rm SO} = \frac{e\hbar}{4m^2c^2}{\bf\sigma} [ {\bf E}({\bf r})\times {\bf p}]},$](img207.png) |
|
|
(3.13) |
leads to a spin-splitting for electrons moving in solids (e.g., semiconductors) even in absence of any magnetic field. Symmetries of the crystal lattice then play a role (Dresselhaus effect), and in artificial heterostructures or quantum wells, an internal electric field
 can give rise to a coupling to the electron spin. This latter case is called Rashba effect.
can give rise to a coupling to the electron spin. This latter case is called Rashba effect.
For a two-dimensional sheet of electrons in the
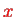 -
-
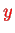 -plane (two-dimensional electron gas, DEG), the simplest case is a Hamiltonian
-plane (two-dimensional electron gas, DEG), the simplest case is a Hamiltonian
![$\displaystyle \hat{H}_{\rm SO} = -\frac{\alpha}{\hbar} \left[ {\bf p} \times {\bf\sigma}\right]_z,$](img211.png) |
|
|
(3.14) |
where the index
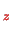 denotes the
denotes the
 component of the operator in the vector
product
component of the operator in the vector
product
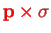 and
and
 is the Rashba parameter. In the case of the hydrogen atom, this factor was determined by the Coulomb potential. In semiconductor structures, it is determined by many factors such as the geometry.
is the Rashba parameter. In the case of the hydrogen atom, this factor was determined by the Coulomb potential. In semiconductor structures, it is determined by many factors such as the geometry.
The Rashba parameter
 can be changed externally by, e.g., applying additional `back-gate' voltages to the structure. This change in
can be changed externally by, e.g., applying additional `back-gate' voltages to the structure. This change in
 then induces a change of the spin-orbit coupling which eventually can be used to manipulate electron spins.
then induces a change of the spin-orbit coupling which eventually can be used to manipulate electron spins.





Next: Perturbation Theory for Fine
Up: Spin-Orbit Coupling
Previous: Spin-Orbit Coupling in Atoms
Contents
Index
Tobias Brandes
2005-04-26
![$\displaystyle {\color{col1}\hat{H}_{\rm SO} = \frac{e\hbar}{4m^2c^2}{\bf\sigma} [ {\bf E}({\bf r})\times {\bf p}]},$](img207.png)
![$\displaystyle {\color{col1}\hat{H}_{\rm SO} = \frac{e\hbar}{4m^2c^2}{\bf\sigma} [ {\bf E}({\bf r})\times {\bf p}]},$](img207.png)
![]() -
-
![]() -plane (two-dimensional electron gas, DEG), the simplest case is a Hamiltonian
-plane (two-dimensional electron gas, DEG), the simplest case is a Hamiltonian
![$\displaystyle \hat{H}_{\rm SO} = -\frac{\alpha}{\hbar} \left[ {\bf p} \times {\bf\sigma}\right]_z,$](img211.png)
![]() can be changed externally by, e.g., applying additional `back-gate' voltages to the structure. This change in
can be changed externally by, e.g., applying additional `back-gate' voltages to the structure. This change in
![]() then induces a change of the spin-orbit coupling which eventually can be used to manipulate electron spins.
then induces a change of the spin-orbit coupling which eventually can be used to manipulate electron spins.