-particle system

Next: Permutations Up: Basis vectors for Fermi Previous: Single Particle Contents Index

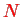$\bgroup\color{col1}$ N$\egroup$ -particle system

We have $\bgroup\color{col1}$ N$\egroup$ particles and 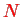$\bgroup\color{col1}$ N$\egroup$ quantum numbers $\bgroup\color{col1}$ \nu_1$\egroup$ ,..., $\bgroup\color{col1}$ \nu_N$\egroup$ . A basis consists of all product states $\bgroup\color{col1}$ \vert\nu_1,...,\nu_N\rangle$\egroup$ corresponding to wave functions $\bgroup\color{col1}$ \psi_{\nu_1}( \xi_1)... \psi_{\nu_N}( \xi_N)$\egroup$ , $\bgroup\color{col1}$ \xi={\bf r}\sigma$\egroup$ ,

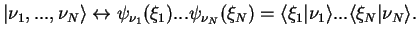$\displaystyle \vert\nu_1,...,\nu_N\rangle \leftrightarrow \psi_{\nu_1}( \xi_1).... ...\nu_N}(\xi_N)=\langle \xi_1\vert\nu_1\rangle ...\langle \xi_N\vert\nu_N\rangle.$

(1.6)

These wave functions still don't have any particular symmetry with respect to permutation of particles. We use them to construct the basis wave functions for Bosons and Fermions.

Tobias Brandes 2005-04-26