




Next: -Fermion systems
Up: Basis vectors for Fermi
Previous: Permutations
Contents
Index
A basis for symmetric wave functions with
 Bosons is constructed in the following way.
Bosons is constructed in the following way.
1. If we just have one possible state
 of the system, the symmetric state and the corresponding wave function is
of the system, the symmetric state and the corresponding wave function is
 |
|
|
(1.11) |
This wave function is obviously symmetric.
2. If we have two particles (
 ), the basis is constructed from the states
), the basis is constructed from the states
 with corresponding wave functions
with corresponding wave functions
 : this product is made symmetric,
: this product is made symmetric,
3. If we just have two possible state
 and
and
 for a system with
for a system with
 particles,
particles,
 particles sit in
particles sit in
 and
and
 particles sit in
particles sit in
 .
We now have to symmetrize the states
.
We now have to symmetrize the states
| |
|
 |
|
| |
|
 |
(1.13) |
If we apply the symmetrization operator
 to this product,
to this product,
 |
|
|
(1.14) |
we get a sum of
 terms, each consisting of
terms, each consisting of
 products of wave functions. For example, for
products of wave functions. For example, for
 and
and
 we get
we get
| |
|
 |
(1.15) |
| |
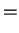 |
 |
(1.16) |
| |
 |
 |
(1.17) |
| |
 |
![$\displaystyle \psi_{\nu_1}(\xi_3) \psi_{\nu_2}(\xi_1) \psi_{\nu_2}(\xi_2) +
\psi_{\nu_1}(\xi_3) \psi_{\nu_2}(\xi_2) \psi_{\nu_2}(\xi_1)\Big],$](img356.png) |
(1.18) |
where in each line in the above equation we have
 identical terms. Had we chosen an example with
identical terms. Had we chosen an example with
 and
and
 , we would have got
, we would have got
 identical terms in each line of the above equation. The symmetrized wave function therefore looks as follows:
identical terms in each line of the above equation. The symmetrized wave function therefore looks as follows:
![$\displaystyle \frac{1}{\sqrt{N!}} N_1! N_2! \left[ \mbox{\rm sum of }\frac{N!}{N_1!N_2!} \quad \mbox{\rm orthogonal wave functions} \right],$](img361.png) |
|
|
(1.19) |
which upon squaring and integrating would give
![$\displaystyle \left[ \frac{1}{\sqrt{N!}} N_1! N_2!\right]^2 \frac{N!}{N_1!N_2!} = N_1!N_2!$](img362.png) |
|
|
(1.20) |
and not one! We therefore need to divide the whole wave function by
 in order to normalise it to one, and therefore the symmetric state with the corresponding normalised, symmetrical wave function is
in order to normalise it to one, and therefore the symmetric state with the corresponding normalised, symmetrical wave function is
This is now easily generalised to the case where we have
 particles in state
particles in state
 ,
,
 particles in state
particles in state
 ,...,
,...,
 particles in state
particles in state
 with
with
 |
|
|
(1.22) |
We then have





Next: -Fermion systems
Up: Basis vectors for Fermi
Previous: Permutations
Contents
Index
Tobias Brandes
2005-04-26
![]() of the system, the symmetric state and the corresponding wave function is
of the system, the symmetric state and the corresponding wave function is

![]() ), the basis is constructed from the states
), the basis is constructed from the states
![]() with corresponding wave functions
with corresponding wave functions
![]() : this product is made symmetric,
: this product is made symmetric,
![$\displaystyle \frac{1}{\sqrt{2}} \left[ \psi_{\nu_1}( \xi_1)\psi_{\nu_2}( \xi_2)
+ \psi_{\nu_1}( \xi_2)\psi_{\nu_2}( \xi_1) \right]$](img342.png)
![]() and
and
![]() for a system with
for a system with
![]() particles,
particles,
![]() particles sit in
particles sit in
![]() and
and
![]() particles sit in
particles sit in
![]() .
We now have to symmetrize the states
.
We now have to symmetrize the states




![$\displaystyle \psi_{\nu_1}(\xi_3) \psi_{\nu_2}(\xi_1) \psi_{\nu_2}(\xi_2) +
\psi_{\nu_1}(\xi_3) \psi_{\nu_2}(\xi_2) \psi_{\nu_2}(\xi_1)\Big],$](img356.png)
![$\displaystyle \frac{1}{\sqrt{N!}} N_1! N_2! \left[ \mbox{\rm sum of }\frac{N!}{N_1!N_2!} \quad \mbox{\rm orthogonal wave functions} \right],$](img361.png)
![$\displaystyle \left[ \frac{1}{\sqrt{N!}} N_1! N_2!\right]^2 \frac{N!}{N_1!N_2!} = N_1!N_2!$](img362.png)



