Direct and Exchange Term: Discussion

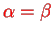1. For $\alpha=\beta$ the anti-symmetrical orbital state vanishes and one has

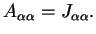$$A_{\alpha\alpha}=J_{\alpha\alpha}.$$ (2.27)

In this case there is only one singlet state and there are no triplet states.

2. Extreme examples for the interaction potential:

$$a)\quad U\left(\vert{\bf r}_1 -{\bf r}_2\vert\right) = U={\rm const}$$

$$\leadsto A_{\alpha\beta} = U,\quad J_{\alpha\beta}=U\delta_{\alpha\beta}$$ (2.28)

$$b) \quad U\left(\vert{\bf r}_1 -{\bf r}_2\vert\right) = U_0\delta({\bf r}_1 -{\bf r}_2)$$

$$\leadsto A_{\alpha\beta}=J_{\alpha\beta} =U_0\int d{\bf r} \vert\phi_\alpha({\bf r})\vert^2 \vert\phi_\beta({\bf r})\vert^2.$$ (2.29)