




Next: Exchange Term
Up: Hartree-Fock Equations
Previous: Hartree-Fock Equations
Contents
Index
The direct term,
direct term![$\displaystyle \quad \left[{\sum_i \int d{\bf r'} \vert\psi_{\nu_{i}}({\bf r'})\vert^2 U(\vert{r-r'}\vert)}\right]\psi_{\nu_{j}}({\bf r})$](img712.png) |
|
|
(3.30) |
acts like a local one-particle potential on particle
 : it depends on all the wave functions
: it depends on all the wave functions
 that have still to be determined. The direct term has a simple physical interpretation: it is the potential at position
that have still to be determined. The direct term has a simple physical interpretation: it is the potential at position
 generated by the total density
generated by the total density
 of all the individual electrons in their states
of all the individual electrons in their states
 at position
at position
 . The direct term can be interpreted as a `direct' re-normalisation of the one-particle Hamiltonian
. The direct term can be interpreted as a `direct' re-normalisation of the one-particle Hamiltonian
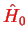 .
.
Tobias Brandes
2005-04-26
![$\displaystyle \quad \left[{\sum_i \int d{\bf r'} \vert\psi_{\nu_{i}}({\bf r'})\vert^2 U(\vert{r-r'}\vert)}\right]\psi_{\nu_{j}}({\bf r})$](img712.png)
![$\displaystyle \quad \left[{\sum_i \int d{\bf r'} \vert\psi_{\nu_{i}}({\bf r'})\vert^2 U(\vert{r-r'}\vert)}\right]\psi_{\nu_{j}}({\bf r})$](img712.png)