Model Hamiltonian

We start from a Hamiltonian describing a system composed of two sub-systems, electrons (e) and nuclei (n)

$$\mathcal{H}= \mathcal{H}_{\rm e}+ \mathcal{H}_{\rm n} + \mathcal{H}_{\rm en},$$ (1.1)

where $\mathcal{H}_{\rm en}$ is the interaction between the two systems. Note that the splitting of the Hamiltonian $\mathcal{H}$ is not unique: for example, $\mathcal{H}_{\rm n}$ could just be the kinetic energy of the nuclei with their mutual interaction potential included into $\mathcal{H}_{\rm en}$ (as in the BO approximation).

The set-up $\mathcal{H}= \mathcal{H}_{\rm e}+ \mathcal{H}_{\rm n} + \mathcal{H}_{\rm en}$ is quite general and typical for so-called `system-bath' theories where one would say the electrons are the `system' and the nuclei are the `bath' (or vice versa!). In the theory of molecules, however, things are a little bit more complicated as there is a back-action of from the electrons on the nuclei. This back-action is due to the electronic charge density acting as a potential for the nuclei.

There is no a priori reason why the nuclei and the electronic system should not be treated on equal footing. However, the theory has a small parameter

$$\kappa=\left(\frac{m}{M}\right)^{\frac{1}{4}}$$ (1.2)

given by the ratio of electron mass $m$ and a typical nuclear mass $M\gg m$, and the exponent $1/4$ is introduced for convenience in the perturbation theory used by Born and Oppenheimer in their original paper. The smallness of this parameter makes it possible to use an approximation which is called the Born-Oppenheimer approximation.

We assume there is a position representation, where $q\equiv \{{\bf x_1},...,{\bf x_N} \}$ represents the positons of all electrons, $X\equiv \{{\bf X_1},...,{\bf X_N} \}$ the positions of all nuclei, and correspondingly for the momenta $p$ and $P$,

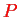$$\mathcal{H}= \mathcal{H}(q,p;X,P)= \mathcal{H}_{\rm e}(q,p)+ \mathcal{H}_{\rm n}(X,P) + \mathcal{H}_{\rm en}(q,X).$$ (1.3)

Spin is not considered here. Also note that the interaction only depends on $(q,X)$ and not on the momenta.