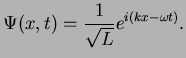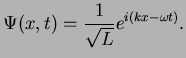Next: Fourier Transforms and the
Up: Interpretation of the Wave
Previous: Probability (2 min)
Contents
Assume that a particle in an interval
![$ [-L/2,L/2]$](img18.png) is described by a wave function
What are the probability density
is described by a wave function
What are the probability density 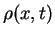 and the current density
and the current density 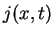 for this wave function ?
How can one express the current density by the probability density and the velocity?
What is the probability to find the particle a) anywhere in the interval
for this wave function ?
How can one express the current density by the probability density and the velocity?
What is the probability to find the particle a) anywhere in the interval
![$ [-L/2,L/2]$](img18.png) ;
b) in the interval
;
b) in the interval ![$ [-L/2,0]$](img22.png) ;
c) in the interval
;
c) in the interval ![$ [0,L/4]$](img23.png) ?
?
Tobias Brandes
2004-02-04