



Next: Expectation values (15 min)
Up: The Infinite Potential Well
Previous: * Orthonormality (10 min)
Contents
Consider a wave function 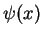 of the infinite potential well on the interval
of the infinite potential well on the interval ![$ [0,L]$](img64.png) .
Consider the case when the wave function at time
.
Consider the case when the wave function at time 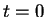 is one of the
eigenstates of energy
is one of the
eigenstates of energy 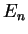 , i.e.
, i.e.
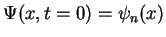 and check that
the time evolution of a wave function that is an energy eigenstate is just given by
multiplication with the time-dependent phase factor
and check that
the time evolution of a wave function that is an energy eigenstate is just given by
multiplication with the time-dependent phase factor
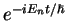 , that is
, that is
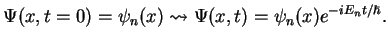 |
|
|
(10) |
Tobias Brandes
2004-02-04