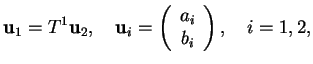Next: Transfer matrix (5 min)
Up: Scattering states in one
Previous: Plane Waves (5 min)
Contents
We consider a 1d piecewise constant potential and
a stationary wave function at energy 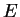 .
.
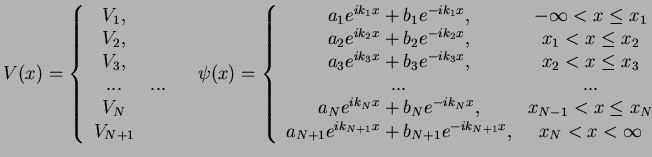 |
(14) |
a) Show that
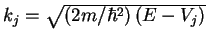 . Discuss the behaviour of
the wave functions in regions with
. Discuss the behaviour of
the wave functions in regions with 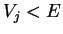 and
and 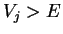 .
.
b) We consider the case
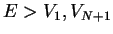 such that
such that 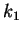 and
and 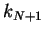 are real wave vectors
and
are real wave vectors
and 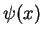 describes running waves outside the `scattering region'
describes running waves outside the `scattering region' ![$ [x_1,x_N]$](img92.png) .
Prove the matrix equation
.
Prove the matrix equation
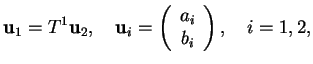 |
(15) |
with
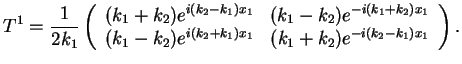 |
(16) |
Tobias Brandes
2004-02-04
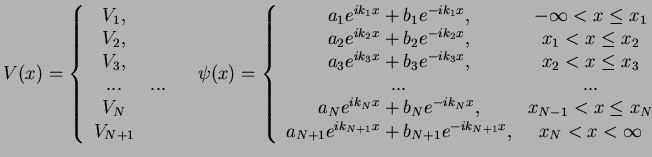
![]() such that
such that ![]() and
and ![]() are real wave vectors
and
are real wave vectors
and ![]() describes running waves outside the `scattering region'
describes running waves outside the `scattering region' ![]() .
Prove the matrix equation
.
Prove the matrix equation