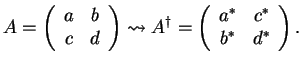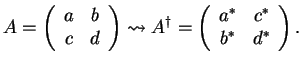Next: Observables (5 min)
Up: Operators and Measurements in
Previous: Definitions (2 min)
Contents
Consider the complex two-dimensional Hilbert space with basis vectors 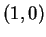 and
and 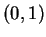 .
Use the definition of the adjoint operator to prove the following for the adjoint
.
Use the definition of the adjoint operator to prove the following for the adjoint
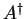 of
the operator
of
the operator 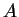 : If
: If 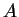 is given as a complex two-by- two matrix,
is given as a complex two-by- two matrix,
Tobias Brandes
2004-02-04