Hamiltonian (10 min)

Next: Ladder Operator (5 min) Up: Ladder Operators and Phonons Previous: Commutator (5 min) Contents

Prove that the Hamiltonian of the one-dimensional harmonic oscillator can be rewritten with the help of ladder operators as

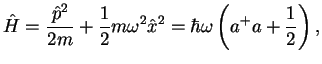$\displaystyle \hat{H}=\frac{\hat{p}^2}{2m}+\frac{1}{2}m\omega^2\hat{x}^2 = \hbar \omega \left( a^+a + \frac{1}{2} \right),$

(39)

Tobias Brandes 2004-02-04