



Next: * Behavior for und
Up: Central Potentials in Three
Previous: Central Potentials in Three
Contents
Show by using the definition of the Laplace operator in polar coordinates and
the definition of the angular momentum square,
![$\displaystyle {\bf\hat{L}}^2=
-\hbar^2 \left[\frac{1}{\sin \theta}\frac{\partia...
...ta}\right)
+\frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2}\right]$](img203.png) |
|
|
(43) |
that the stationary Schrödinger equation for energy 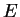 for the motion of a particle with mass
for the motion of a particle with mass
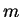 in a central potential
in a central potential 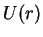 can be separated with the Ansatz
for the wave function
can be separated with the Ansatz
for the wave function
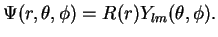 |
(44) |
In order to do so, define the radial function
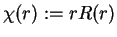 and show
and show
![$\displaystyle \frac{d^2\chi(r)}{dr^2}+\left[\frac{2m}{\hbar^2}(E-U(r))-\frac{l(l+1)}{r^2}\right]\chi(r)=0.$](img207.png) |
(45) |
Which values are possible for 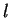 (without proof)?
(without proof)?
Tobias Brandes
2004-02-04
![$\displaystyle {\bf\hat{L}}^2=
-\hbar^2 \left[\frac{1}{\sin \theta}\frac{\partia...
...ta}\right)
+\frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2}\right]$](img203.png)
![$\displaystyle {\bf\hat{L}}^2=
-\hbar^2 \left[\frac{1}{\sin \theta}\frac{\partia...
...ta}\right)
+\frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2}\right]$](img203.png)