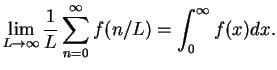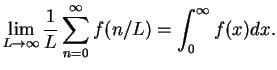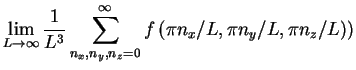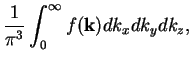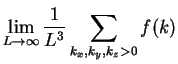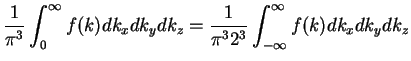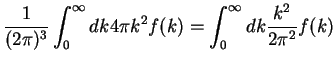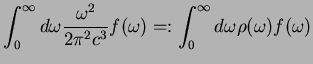Next: Waves, particles, and wave
Up: The Radiation Laws and
Previous: Remarks
Contents
A math theorem tells that for a function 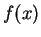 ,
,
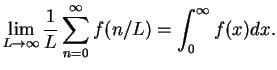 |
(8) |
Assume standing waves in a box of size 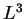 with wave vectors
Assume we wish to calculate a function
with wave vectors
Assume we wish to calculate a function
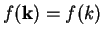 that only depends on the modulus of
that only depends on the modulus of 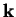 .
We use
.
We use
i.e.
Here,
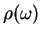 is the density of states if there was only one polarization direction per possible `state'
(wave vector
is the density of states if there was only one polarization direction per possible `state'
(wave vector 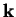 ). If there are two polarization directions, like for unpolarized light,
the density of states is twice as large, i.e.
). If there are two polarization directions, like for unpolarized light,
the density of states is twice as large, i.e.
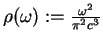 .
.




Next: Waves, particles, and wave
Up: The Radiation Laws and
Previous: Remarks
Contents
Tobias Brandes
2004-02-04