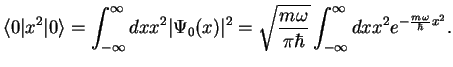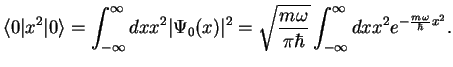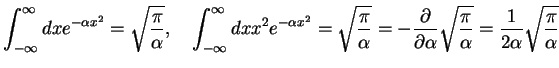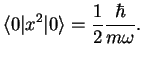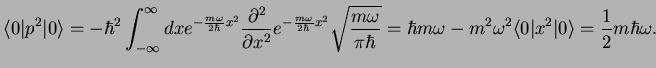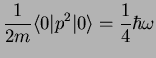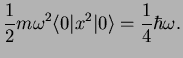Harmonic Oscillator: Expectation Values

We calculate the ground state expectation values

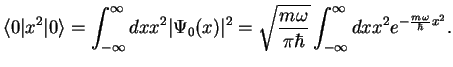$$\langle 0\vert x^2 \vert\rangle = \int_{-\infty}^{\infty}dx x^2 \... ...{m\omega}{\pi\hbar}}\int_{-\infty}^{\infty}dx x^2e^{-\frac{m\omega}{\hbar}x^2}.$$ (257)

This integral is evaluated using

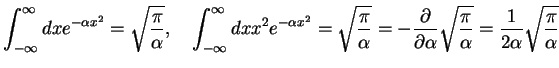$$\int_{-\infty}^{\infty}dxe^{-\alpha x^2}=\sqrt{\frac{\pi}{\alpha}... ...l \alpha}\sqrt{\frac{\pi}{\alpha}} = \frac{1}{2\alpha}\sqrt{\frac{\pi}{\alpha}}$$ (258)

(integration by differentiation). Therefore,

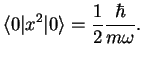$$\langle 0\vert x^2 \vert\rangle = \frac{1}{2}\frac{\hbar}{m\omega}.$$ (259)

Similarily,

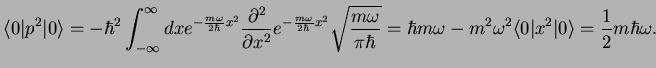$$\langle 0\vert p^2 \vert\rangle = -\hbar^2 \int_{-\infty}^{\infty... ...mega - m^2 \omega^2 \langle 0\vert x^2 \vert\rangle= \frac{1}{2}m \hbar \omega.$$ (260)

Using this, we can calculate the expectation value of the potential and the kinetic energy in the ground state,

$$\langle 0 \vert E_{\rm kin} \vert \rangle = \frac{1}{2m}\langle 0\vert p^2 \vert\rangle = \frac{1}{4}\hbar \omega$$

$$\langle 0 \vert E_{\rm pot} \vert \rangle = \frac{1}{2}m\omega^2\langle 0\vert x^2 \vert\rangle = \frac{1}{4}\hbar \omega.$$ (261)

Note that we have 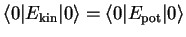$\langle 0 \vert E_{\rm kin} \vert \rangle=\langle 0 \vert E_{\rm pot} \vert \rangle$ (Virial theorem).