




Next: Rates and Energy Shift
Up: Master Equation (RWA)
Previous: Master Equation (RWA)
Contents
Index
The bath correlation functions simply are
where all the information on the microscopic coupling to the bath
in now comprised within one single function,
the bath spectral density
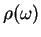
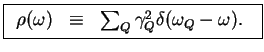 |
|
|
(37) |
Using
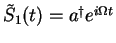 ,
,
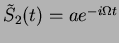 ,
we have
,
we have
Here, we defined the Laplace transformation of a function 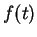 ,
,
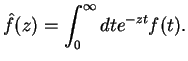 |
|
|
(39) |
The Master equation therefore is





Next: Rates and Energy Shift
Up: Master Equation (RWA)
Previous: Master Equation (RWA)
Contents
Index
Tobias Brandes
2004-02-18
![$\displaystyle {\rm Tr}_B \left[\tilde{B}_1(t){B}_2R_0\right]
= {\rm Tr}_B \left[\sum_{QQ'}\gamma_Q\gamma_{Q'}a_Qe^{-i\omega_Q t}
a^{\dagger}_{Q'}R_0\right]$](img144.png)
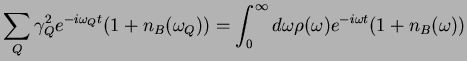
![$\displaystyle {\rm Tr}_B \left[\tilde{B}_2(t){B}_1R_0\right]
= {\rm Tr}_B \left[\sum_{QQ'}\gamma_Q\gamma_{Q'}a_Q^{\dagger}e^{i\omega_Q t}
a_{Q'}R_0\right]$](img147.png)
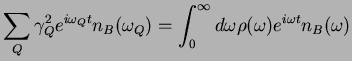
![]() ,
,
![]() ,
we have
,
we have
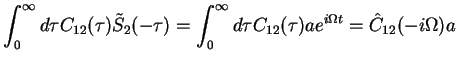
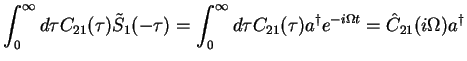
![$\displaystyle \int_0^{\infty}d \tau C_{21}^*(\tau)\tilde{S}_2(-\tau)=
\int_0^{\...
...\tau C_{21}^*(\tau) ae^{i\Omega t}
= [\hat{C}_{21}(i\Omega)]^* a =D_2^{\dagger}$](img159.png)
![$\displaystyle \int_0^{\infty}d \tau C_{12}^*(\tau)\tilde{S}_1(-\tau)=
\int_0^{\...
...^{\dagger}e^{-i\Omega t}
= [\hat{C}_{12}(-i\Omega)]^* a^{\dagger}=D_1^{\dagger}$](img161.png)
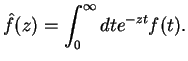
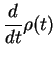
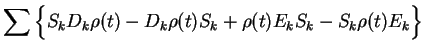
![$\displaystyle \Big\{ \left[\hat{C}_{12}(-i\Omega)a^{\dagger} a + \hat{C}_{21}(i...
...{21}(i\Omega)]^*a a^{\dagger} + [\hat{C}_{12}(-i\Omega)]^* a^{\dagger} a\right]$](img167.png)
![$\displaystyle \hat{C}_{12}(-i\Omega) a{\rho}(t)a^{\dagger}
-\hat{C}_{21}(i\Omeg...
...\dagger}{\rho}(t) a
- [\hat{C}_{12}(-i\Omega)]^*a {\rho}(t) a^{\dagger}
\Big\}.$](img168.png)