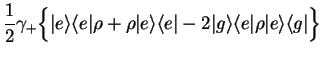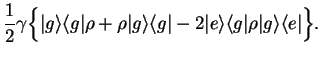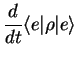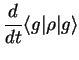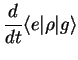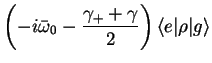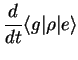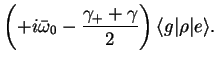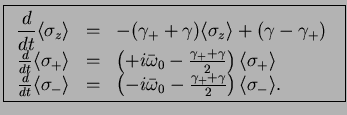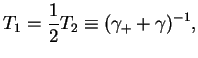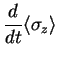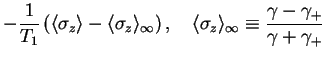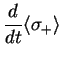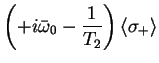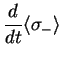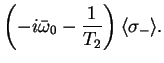Next: The Quantum Jump (Quantum
Up: The Two-Level System I
Previous: Mapping onto harmonic oscillator
Contents
Index
We can write the Master equation with the help of
Taking matrix elements, we obtain
The first two equations for the diagonal elements
(which are linearly dependent because
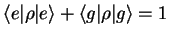 ) are called Einstein equations.
We can re-write the four equations, subtracting the second from the first, as
three equations,
) are called Einstein equations.
We can re-write the four equations, subtracting the second from the first, as
three equations,
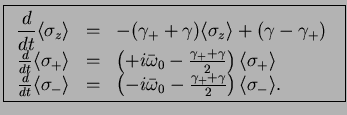 |
|
|
(135) |
These equations are called Bloch equations.
Introducing the relaxation time 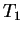 and the decoherence time
and the decoherence time 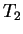 ,
,
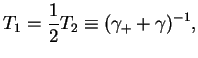 |
|
|
(136) |
we can write





Next: The Quantum Jump (Quantum
Up: The Two-Level System I
Previous: Mapping onto harmonic oscillator
Contents
Index
Tobias Brandes
2004-02-18
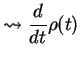
![$\displaystyle -i\frac{1}{2}\bar{\omega}_0[\vert e\rangle\langle e\vert-\vert g\rangle\langle g\vert,\rho]$](img578.png)
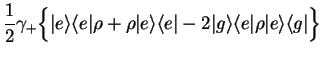
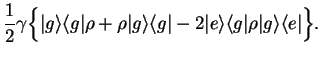
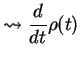
![$\displaystyle -i\frac{1}{2}\bar{\omega}_0[\vert e\rangle\langle e\vert-\vert g\rangle\langle g\vert,\rho]$](img578.png)