




Next: Quantum Oscillations in Two-Level
Up: Example: Two-Level System
Previous: Power Series
Contents
Index
We diagonalise
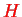 according to
according to
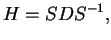 |
|
|
(1.13) |
where
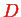 is the diagonal matrix of the eigenvalues and
is the diagonal matrix of the eigenvalues and
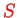 the orthogonal matrix of the eigenvectors.
This yields
the orthogonal matrix of the eigenvectors.
This yields
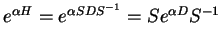 |
|
|
(1.14) |
which follows from the definition of the power series (Exercise: CHECK)!
For
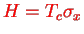 , we already calculated the EVs in an earlier chapter,
, we already calculated the EVs in an earlier chapter,
with
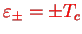 . Thus,
. Thus,





Next: Quantum Oscillations in Two-Level
Up: Example: Two-Level System
Previous: Power Series
Contents
Index
Tobias Brandes
2005-04-26
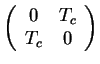
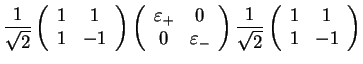
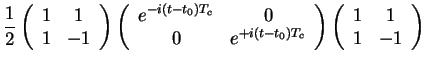
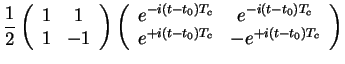
![$\displaystyle \left(\begin{array}{cc}
\cos [(t-t_0)T_c] & -i \sin [(t-t_0)T_c] \\
-i \sin [(t-t_0)T_c] & \cos [(t-t_0)T_c] \\
\end{array}\right)$](img1056.png)